上机实验(初识 Python)
-
每个人在自带电脑上安装 Python 编程环境(包括安装 Python 解释器和 Visual Studio Code 编辑器,并在后者中安装 Python 开发相关扩展)。最后通过如下命令打印你所安装的 Python 版本信息:
% python --version参考资料:搭建 Python 开发环境
-
熟悉 Python 的交互式执行环境,在交互式模式下打印 Python 之禅。
-
请在交互式模式下进行如下运算:
已知 a = 3.4, b = -2.3, c = 18.9,且有抛物线方程:
$$y=ax^2+bx+c$$
请在交互式模式下,分别计算当 x = -3.8 和 x = 49.0 时的函数值 y,并显示计算结果。
-
初步掌握
print()函数的用法,请运行如下代码,并观察运行结果:print("人生苦短,我用 Python") pi = 3.14000000 print("π 值:", pi) pi = 3.14159265358979323846264338327950288419716939937510582097494459 print(pi) print("《登鹳雀楼》\n——王之涣\n白日依山尽,黄河入海流。\n欲穷千里目,更上一层楼。\n") -
熟悉 Python 编程的源文件模式,利用 VS Code 或 PyCharm 编写代码实现将角度值 30.05° 转换为弧度值,并打印显示计算结果。
-
直角梯形绕着垂直底边的腰旋转一周所得的几何体称为圆台,如图 1 所示。其中 r1 为下底面半径,r2 为上底面半径,h 为高,s 为母线长度(腰长)。
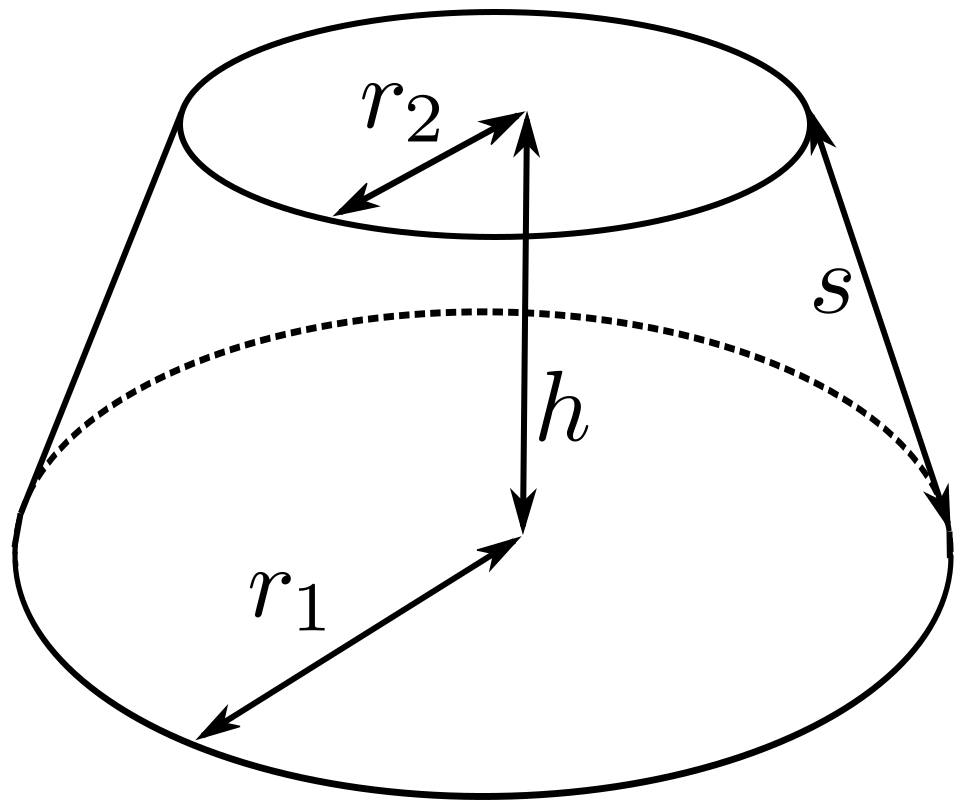
圆台 已知圆台的各项参数计算公式为:
母线长
$$s=\sqrt{h^2+\left( r_1-r_2 \right) ^2}$$
侧面积
$$A_l=\pi \left( r_1+r_2 \right) s$$
全面积
$$A_t=\pi \left[ \left( r_1+r_2 \right) s+r_{1}^{2}+r_{2}^{2} \right]$$
体积
$$V=\frac{\pi h}{3}\left( r_{1}^{2}+r_1r_2+r_{2}^{2} \right)$$
对某圆台,给定如下参数,并计算其母线长:
r1 = 15.0 # 下底面半径 r2 = 10.0 # 上底面半径 h = 9.3 # 高 pi = 3.141592653589793 # π 值 s = (h**2 + (r1 - r2)**2)**0.5 # 母线长 print("圆台的母线长为:", s)请参考上述计算和打印母线长的方法进一步计算和打印圆台的侧面积、全面积和体积。
-
请在脱离 VS Code 或 PyCharm 的条件下,使用如下方式运行上一题所编写的 Python 源代码文件:
% python C:\path\to\py-file.py注意,需要将这里的
C:\path\to\py-file.py变为实际的文件路径。