1. NumPy 介绍

1.1 概述

Numpy（发音 /ˈnʌmpaɪ/）是一个 Python 语言库，它提供了对大型、多维数组（或称矩阵）的支持，以及大量的操作这些数组的高级数学函数，包括数学、逻辑、形状操作、排序、选择、I/O、离散傅立叶变换、基本线性代数、基本统计运算、随机模拟等等。

前往 NumPy 官方网站，以及 NumPy 中文文档。

1.2 NumPy 的特色

• 强大的多维数组：NumPy 的向量化、索引和广播的理念是当今数组操作事实上的标准，使其变得快速且全功能。
• 数值计算工具：NumPy 提供了各种数学函数、随机数生成器、线性代数例程、傅里叶变换，等等。
• 开源：NumPy 在 BSD 协议下发布，并且在 GitHub 上由一个充满生机、热情和多样化的社区共同维护。
• 可互操作性强：NumPy 支持大量的硬件和计算平台，能很好地分布式、GPU 和稀疏数组库上的计算。
• 易于使用：NumPy 的高级语法让具有各种背景和经验等级的程序员都能掌握和高效使用。

1.2 NumPy 的特色

与 MATLAB 比较：

• NumPy 的功能与 MATLAB 类似，他们都是解释执行的，并且都允许用户快速编写针对数组或矩阵的程序。
• MATLAB 的主要优势在于具有大量额外的工具箱，如著名的 Simulink；NumPy 的主要优势是与 Python 完全整合在一起，而 Python 是一个现代的和全功能的编程语言。
• 有大量的 Python 包可以补全 NumPy 的功能，如 SciPy 包补充了许多类似 MATLAB 的函数，Matplotlib 包提供了类似 MATLAB 的绘图功能。
• MATLAB 和 NumPy 都同样依赖 BLAS（基础线性代数程序集，Basic Linear Algebra Subprograms）和LAPACK（线性代数包，Linear Algebra PACKage），从而可以高效地进行线性代数计算。

1.3 安装 NumPy？

如果你使用的包管理工具为 pip，则可以通过如下命令安装 NumPy：

$ pip install numpy

如果使用 conda，则可以使用如下命令从 defaults 或 conda-forge 频道安装 NumPy：

# 最佳实践，创建一个新环境而不是在基础的 env 环境中安装
$ conda create -n my-env
$ conda activate my-env
# 配置从 conda-forge 安装
$ conda config --env --add channels conda-forge
# 实际的安装命令
conda install numpy

1.4 NumPy 数组介绍

NumPy 包的核心是 ndarray 对象，即 NumPy 数组。该对象封装了相同类型数据构成的多维数组，为了提高性能，许多操作都在编译后的代码中执行。NumPy 数组和标准 Python 序列之间的最重要区别包括：

❶ NumPy 数组在创建时具有固定的尺寸，不像 Python 列表具有动态的尺寸。改变 ndarray 的尺寸将创建一个新数组，并删除原有数组。

❷ NumPy 数组的所有元素必须是相同类型的，因此将占据相同尺寸的内存。但有一个例外：NumPy 元素类型可以是 Python 或 NumPy 的数组对象，各个数组可以有不同的元素数量。

1.4 NumPy 数组介绍

❸ NumPy 数组擅长对大量数据实施高级的数学或其他类型的操作。与使用 Python 内建的序列相比，这种操作的执行效率更高，代码更少。

❹ 越来越多的基于 Python 的科学和数学包都使用 NumPy 数组；虽然这些包通常支持以 Python 序列作为输入，但在运算前都会将输入转换为 NumPy 数组，经常也输出 NumPy 数组。换句话说，为了有效地使用当今许多（甚至可能是大多数）基于 Python 的科学/数学软件，仅仅知道如何使用 Python 的内置序列类型是不够的——还需要知道如何使用 NumPy 数组。

1.4 NumPy 数组介绍

在科学计算中，序列的大小和速度是非常重要的。考虑将一个一维序列中的每个元素与另一个相同长度序列中的对应元素相乘的简单示例，如果将数据都存储在 Python 列表类型变量 a 和 b 中，则应该按照如下方法进行迭代：

a = [x for x in range(100)]
b = [x*x for x in range(100)]
c = []
for i in range(len(a)):
    c.append(a[i]*b[i])

这种方法是正确的，但如果 a 和 b 包含数以百万计的元素，这种不断地往 c 中追加元素的效率是极其低下的。在其他一些更偏重底层控制的语言（如 C 语言）中，这种问题却能较容易地被解决。

1.4 NumPy 数组介绍

通过使用 NumPy，在涉及有关 ndarray 类型中需要进行逐个元素遍历操作时，可以按照惯常的 Python 方式操作，同时又以预编译的 C 代码快速执行。对于以上示例，使用 NumPy 后可写作：

import numpy as np

a = np.array([x for x in range(100)])
b = np.array([x*x for x in range(100)])
c = a * b

这行代码所做的事情与前面的代码相同，看上去更简单，但却可以以接近 C 语言的速度执行。这个例子揭示了 NumPy 的两个特征：矢量化（vectorization）和广播（broadcasting）——他们是 NumPy 大部分功能的基础。

1.4 NumPy 数组介绍

围绕 ndarray，NumPy 完全支持面向对象的编程方式。ndarray 是一个类，拥有大量方法和属性。它的许多方法都被镜像到 NumPy 命名空间的最外层函数，从而使程序员可以用他们偏爱的范式进行编码。

这种灵活性使 NumPy ndarray 类成为在 Python 中进行多维数据交换的事实标准，NumPy 也成为用 Python 进行科学计算的基础包。

1.5 矢量化和广播

矢量化可以使代码中不出现任何显式的循环和索引，这些是预编译的 C 代码在“幕后”优化的结果。矢量化代码具有如下优点：

• 矢量化代码更简洁，更易于阅读；
• 更少的代码行通常意味着更少的错误；
• 代码更接近于标准的数学符号，因此也更容易基于数学语言编写正确的代码；
• 矢量化使我们更容易编写地道的 Python 风格的代码，避免代码被低效且难以阅读的 for 循环弄得一团糟。

1.5 矢量化和广播

广播是用于描述操作以隐式的逐元素进行的术语。一般来说，NumPy 的所有操作，不光算术运算，还包括逻辑、位、功能等，都表现为这种隐式的逐元素进行的行为，即他们进行了广播。此外，在以上示例中，a 和 b 可以是相同形状的多维数组，或者同为标量或同为数组，甚至是不同形状的数组，条件是较小的数组可以“扩展”到更大的形状，以此保证广播能明确无误地进行。

2. 基础知识

2.1 ndarray 对象介绍

NumPy 的主要对象是同构的多维数组。它是一个同类型元素（通常是数字）构成的表，由非负整数元组索引。NumPy 中的维度被称为轴（axes）。

例如，3D 空间中的点坐标 [1, 2, 1] 具有一个轴。该轴有 3 个元素，因此我们说它的长度为 3。在如下示例中，数组有 2 个轴。第一轴的长度为 2，第二轴的长度为 3。

[[ 1., 0., 0.],
 [ 0., 1., 2.]]

NumPy 的数组类被称作 ndarray，它具有别名 array。请注意，numpy.array 与 Python 标准库中的 array.array 类并不相同，后者只处理一维数组并提供较少的功能。

2.1 ndarray 对象介绍

以下列出了 ndarray 对象的一些重要属性：

• ndarray.ndim：数组的轴（维度）的个数。
• ndarray.shape：数组的维度。这是一个整数元组，表示每个维度中数组的大小。对于有 n 行和 m 列的矩阵，shape 为 (n,m)。因此，shape 元组的长度就是轴的个数 ndim。
• ndarray.size：数组元素的总数。这等于 shape 中各元素的乘积。
• ndarray.dtype：一个描述数组中元素类型的对象。可以使用标准的 Python 类型创建或指定 dtype。另外 NumPy 也提供它自己的类型，如 numpy.int32、numpy.int16 和 numpy.float64。
• ndarray.itemsize：数组中每个元素占用的字节数。例如，元素为 float64 类型的数组的 itemsize 为 8（=64/8），而 complex32 类型的数组的 itemsize 为 4（=32/8）。该值与 ndarray.dtype.itemsize 相等。
• ndarray.data：包含实际数组元素的缓冲区。由于可以通过索引机制访问数组中的元素，因此通常不需要使用此属性。

2.1 ndarray 对象介绍

一个例子：

import numpy as np

# arange() 类似于 Python 内建的 range(), 但返回 ndarray 对象；
# reshape() 将 ndarray 对象变为特定维度的对象，并返回该 ndarray 对象
a = np.arange(15).reshape(3, 5)

print(a)
# [[ 0  1  2  3  4]
#  [ 5  6  7  8  9]
#  [10 11 12 13 14]]

print(a.shape)  # (3, 5)
print(a.ndim)  # 2
print(a.dtype.name)  # int64
print(a.itemsize)  # 4
print(a.size)  # 15
print(type(a))  # <class 'numpy.ndarray'>

b = np.array([6, 7, 8])
print(b)  # [6 7 8]
print(type(b))  # <class 'numpy.ndarray'>

2.2 创建数组

有多种创建数组的方法，请查看创建数组函数文档了解详细信息。

❶ 使用 array 函数从常规的 Python 列表或元组创建数组

numpy.array(object, dtype=None, *, copy=True, 
            order='K', subok=False, ndmin=0, like=None)

import numpy as np

a = np.array([2, 3, 4])
print(a)  # [2 3 4]
print(a.dtype)  # int32
b = np.array([1.2, 3.5, 5.1])
print(b.dtype)  # float64

所得数组元素的类型是从序列元素的类型自动推导得出的。

2.2 创建数组

❶ 使用 array 函数从常规的 Python 列表或元组创建数组

使用 array 函数的一个常见错误是在调用时为其提供了多个参数，而不是提供单个序列参数：

import numpy as np

a = np.array(1, 2, 3, 4)  # 错误
# TypeError: array() takes from 1 to 2 positional arguments but 4 were given

a = np.array([1, 2, 3, 4])  # 正确
a = np.array((1, 2, 3, 4))  # 正确

2.2 创建数组

❶ 使用 array 函数从常规的 Python 列表或元组创建数组

array 函数可以将序列的序列转换为二维数组，将序列的序列的序列转换为三维数值，依次类推；还可以在 array 的参数中显式指定元素类型：

import numpy as np

b = np.array([(1.5, 2, 3), (4, 5, 6)])
print(b)
# [[1.5 2.  3. ]
#  [4.  5.  6. ]]

c = np.array([[1, 2], [3, 4]], dtype=complex)
print(c)
# [[1.+0.j 2.+0.j]
#  [3.+0.j 4.+0.j]]

2.2 创建数组

❷ 用特定函数创建具有特定尺寸和初始元素值的数组

• zeros：通过给定形状和类型创建数组，并用 0 填充元素值。

  numpy.zeros(shape, dtype=float, order='C', *, like=None)

• ones：通过给定形状和类型创建数组，并用 1 填充元素值。

  numpy.ones(shape, dtype=None, order='C', *, like=None)

• empty：通过给定形状和类型创建数组，同时不初始化元素值。

  numpy.empty(shape, dtype=float, order='C', *, like=None)

• full：创建一个具有给定形状和类型的数组，并用给定的 fill_value 值填充各元素。

  numpy.full(shape, fill_value, dtype=None, order='C', *, like=None)

2.2 创建数组

❷ 用特定函数创建具有特定尺寸和初始元素值的数组

import numpy as np

print(np.zeros((3, 4)))  # 不指定 dtype 值时，默认类型是 float64
# [[0. 0. 0. 0.]
#  [0. 0. 0. 0.]
#  [0. 0. 0. 0.]]
print(np.ones((2, 3, 4), dtype=np.int16))  # 显式指定 dtype 值
# [[[1 1 1 1]
#   [1 1 1 1]
#   [1 1 1 1]]

#  [[1 1 1 1]
#   [1 1 1 1]
#   [1 1 1 1]]]
print(np.empty((2, 3)))
# [[1.39069238e-309 1.39069238e-309 1.39069238e-309]
#  [1.39069238e-309 1.39069238e-309 1.39069238e-309]]

2.2 创建数组

❸ 使用 arange 和 linspace 函数创建数组

arange 函数与 Python 内建的 range 函数类似，但返回 ndarray 对象。

numpy.arange([start, ]stop, [step, ]dtype=None, *, like=None)

import numpy as np

print(np.arange(10, 30, 5))  # [10 15 20 25]
print(np.arange(0, 2, 0.3))  # [0.  0.3 0.6 0.9 1.2 1.5 1.8]

2.2 创建数组

❸ 使用 arange 和 linspace 函数创建数组

当 arange 与浮点参数一起使用时，由于有限的浮点精度，通常不可能预测所获得的元素的数量。出于这个原因，通常最好使用 linspace 函数来显式指定我们想要的元素数量，而不是像 arange 函数那样指定步长：

numpy.linspace(start, stop, num=50, endpoint=True,
            retstep=False, dtype=None, axis=0)

import numpy as np

print(np.linspace(0, 2, 9))  # [0.   0.25 0.5  0.75 1.   1.25 1.5  1.75 2.  ]
print(np.linspace(0, 2 * np.pi, 30))
# [0.         0.21666156 0.43332312 0.64998469 0.86664625 1.08330781
#  1.29996937 1.51663094 1.7332925  1.94995406 2.16661562 2.38327719
#  2.59993875 2.81660031 3.03326187 3.24992343 3.466585   3.68324656
#  3.89990812 4.11656968 4.33323125 4.54989281 4.76655437 4.98321593
#  5.1998775  5.41653906 5.63320062 5.84986218 6.06652374 6.28318531]

2.2 创建数组

还有更多的创建数组的函数。该页面把创建数组的函数分为多个分类：从形状或值创建、从已有数据创建、创建记录数组 numpy.rec、创建字符数组 numpy.char、数值范围、构建矩阵、矩阵类。

注意该页面许多函数具有 _like 后缀，如 zeros_like、ones_like、empty_like、full_like，这些函数的功能和不带 _like 的函数类似，但可不必为其提供 shape 和 dtype 参数，而可通过为其提供一个原型数组 a，从而创建与该原型具有相同形状和类型的数组。

实际创建数组时，应根据具体场景，从该页面选择使用合适的函数。

2.3 基本操作

根据矢量化和广播规则，对数组的算术运算符会逐个应用到每个元素。下面是创建一个新数组并填充结果的示例：

import numpy as np

a = np.array([20, 30, 40, 50])
b = np.arange(4)
c = a - b
print(c)  # [20 29 38 47]
print(b**2)  # [0 1 4 9]
print(10 * np.sin(a))  # [ 9.12945251 -9.88031624  7.4511316  -2.62374854]
print(a < 35)  # [ True  True False False]

2.3 基本操作

与许多矩阵运算语言不同，乘法运算符 * 在 NumPy 数组中是逐个元素进行。矩阵乘积可以使用 @ 运算符（对 Python >= 3.5）或 dot 函数或方法执行：

import numpy as np
A = np.array( [[1,1], [0,1]] )
B = np.array( [[2,0], [3,4]] )
print(A * B)
# [[2 0]
#  [0 4]]

print(A @ B)
print(A.dot(B))
print(np.dot(A, B))
# 结果均为：
# [[5 4]
#  [3 4]]

2.3 基本操作

某些操作（例如 += 和 *=）会更直接更改被操作的矩阵数组而不会创建新矩阵数组。

import numpy as np

a = np.ones((2,3), dtype=int)
b = np.random.random((2,3))
a *= 3
print(a)
# [[3 3 3]
#  [3 3 3]]
b += a
print(b)
# [[3.42596777 3.14670933 3.10927589]
#  [3.64844792 3.381072   3.46206654]]
a += b  # b 的元素是浮点类型，无法被自动转换为 a 的整数类型
# numpy.core._exceptions._UFuncOutputCastingError: Cannot cast ufunc 'add' output from dtype('float64') to dtype('int32') with casting rule 'same_kind'

2.3 基本操作

当对不同类型的数组进行操作时，会遵守向上转换的规则，即结果数组的类型将是参与运算的类型中更一般和更通用的类型。

import numpy as np

a = np.ones(3, dtype=np.int32)
b = np.linspace(0, np.pi, 3)
print(b.dtype.name)  # float64

c = a + b
print(c, c.dtype.name)  # [1.         2.57079633 4.14159265] float64

d = np.exp(c*1j)
print(d, d.dtype.name)  # [ 0.54030231+0.84147098j -0.84147098+0.54030231j -0.54030231-0.84147098j] complex128

2.3 基本操作

许多一元运算，如计算数组中所有元素的和，都是作为 ndarray 类的方法实现的。

import numpy as np

rng = np.random.default_rng()  # 创建一个伪随机数生成器
a = rng.random((2, 3))
print(a)
# [[0.54981685 0.85835019 0.50779762]
#  [0.54727067 0.92390732 0.83417839]]

print(a.sum(), a.max(), a.min())
# 4.2213210430646395 0.9239073221612277 0.5077976241685102

2.3 基本操作

默认情况下，适用于数字列表的运算也适用于任何形状的数组。不过，通过指定 axis 参数，您可以沿数组的指定轴进行运算：

import numpy as np

b = np.arange(12).reshape(3, 4)
print(b)
# [[ 0  1  2  3]
#  [ 4  5  6  7]
#  [ 8  9 10 11]]

print(b.sum(axis=0))  # 每列之和
# [12 15 18 21]

print(b.min(axis=1))  # 每行的最小值
# [0 4 8]

print(b.cumsum(axis=1))  # 沿每行的累加和
# [[ 0  1  3  6]
#  [ 4  9 15 22]
#  [ 8 17 27 38]]

2.4 通用函数

NumPy 提供了一些我们原来已熟悉的数学函数，如 sin，cos 和 exp。在 NumPy 中，这些被称为“通用函数”（ufunc），这些函数在数组上按元素逐个进行运算，产生一个数组作为输出。

import numpy as np

a = np.arange(3)
b = np.array([2., -1., 4.])
print(a)  # [0 1 2]

print(np.exp(a))  # [1.         2.71828183 7.3890561 ]
print(np.sqrt(a))  # [0.         1.         1.41421356]
print(np.add(a, b))  # [2. 0. 6.]

2.4 通用函数

其他常见的通用函数包括：

all, any, apply_along_axis, argmax, argmin, argsort, average, bincount, ceil, clip, conj, corrcoef, cov, cross, cumprod, cumsum, diff, dot, floor, inner, invert, lexsort, max, maximum, mean, median, min, minimum, nonzero, outer, prod, re, round, sort, std, sum, trace, transpose, var, vdot, vectorize, where

2.5 索引、切分和迭代

可以像对待 Python 序列一样对一维数组进行索引、切分和迭代。

import numpy as np

a = np.arange(10)**3
print(a)  # [  0   1   8  27  64 125 216 343 512 729]
print(a[2:5])  # [ 8 27 64]
# 等价于 a[0:6:2] = 1000，从开始到 6,将每第二个元素值设置为 1000
a[:6:2] = 1000
print(a)  # [1000    1 1000   27 1000  125  216  343  512  729]
print(a[::-1])  # a 的逆序数组
# [ 729  512  343  216  125 1000   27 1000    1 1000]
for e in a:
    print(e**(1 / 3.))
# 9.999999999999998
# 1.0
# 9.999999999999998
# 3.0
# 9.999999999999998
# 4.999999999999999
# 5.999999999999999
# 6.999999999999999
# 7.999999999999999
# 8.999999999999998

2.5 索引、切分和迭代

多维数组的每个轴都可以有一个索引，这些索引以逗号分隔的元组给出（注意这与 Python 的多维列表或元组的方法不同）。

import numpy as np

def f(x, y):
    return 10 * x + y

# fromfunction 通过针对每个元素执行一次函数而构建数组
b = np.fromfunction(f, (5, 4), dtype=int)
print(b)
# [[ 0  1  2  3]
#  [10 11 12 13]
#  [20 21 22 23]
#  [30 31 32 33]
#  [40 41 42 43]]

print(b[2, 3])  # 23

# 以下两行均打印 a 的所有列的第二行
print(b[0:5, 1])
print(b[:, 1])
# [ 1 11 21 31 41]

print(b[1:3, :])  # a 的第 2、3 行的所有列
# [[10 11 12 13]
#  [20 21 22 23]]

2.5 索引、切分和迭代

当提供的索引数少于轴的数量时，缺失的索引被认为是完整的切片：

print(b[-1])  # 最后一行，等价于 b[-1, :]
# [40 41 42 43]

b[i] 方括号中的表达式 i 被视为后面紧跟着足够多的 :，用于表示剩余轴。NumPy 也允许将省略的轴表示为三个点（不是省略号），如 b[i, ...]。三个点（...）代表生成完整的索引元组所需的冒号。

例如，假设 x 是一个具有 5 个轴的数组，则：

• x[1, 2, ...] 等价于 x[1, 2, :, :, :]；
• x[..., 3] 等价于 x[:, :, :, :, 3]；
• x[4, ..., 5, :] 等价于 x[4, :, :, 5, :]。

2.5 索引、切分和迭代

一个更复杂的示例：

import numpy as np

c = np.array([[[  0,  1,  2],  # 一个三维数组
                [ 10, 12, 13]],
                [[100, 101, 102],
                [110, 112, 113]]])

print(c.shape)  # (2, 2, 3)

print(c[1, ...])  # c[1, ...] 等价于 c[1, :, :] 或 c[1]
# [[100 101 102]
#  [110 112 113]]

print(c[..., 2])  # c[..., 2] 等价于 c[:, :, 2]
# [[  2  13]
#  [102 113]]

2.5 索引、切分和迭代

对多维数组进行迭代操作是针对第一个轴进行的：

import numpy as np
b = np.array([[ 0,  1,  2,  3],
              [10, 11, 12, 13],
              [20, 21, 22, 23],
              [30, 31, 32, 33],
              [40, 41, 42, 43]])
for row in b:
    print(row)
# [0 1 2 3]
# [10 11 12 13]
# [20 21 22 23]
# [30 31 32 33]
# [40 41 42 43]

2.5 索引、切分和迭代

如果想要对数组中的每个元素执行操作，可以使用 flat 属性，该属性是数组的所有元素的迭代器：

import numpy as np
b = np.array([[ 0,  1,  2,  3],
                [10, 11, 12, 13],
                [20, 21, 22, 23],
                [30, 31, 32, 33],
                [40, 41, 42, 43]])
for element in b.flat:
    print(element)
# 0
# 1
# 2
# 3
# 10
# 11
# 12
# 13
# 20
# 21
# 22
# 23
# 30
# 31
# 32
# 33
# 40
# 41
# 42
# 43

3. 形状操作

3.1 改变数组的形状

一个数组的形状是由每个轴的元素数量决定的。可以通过多种方式改变数组的形状，以下介绍常用的函数或方法。

最常用的形状操作是获得一个数组（一般是二维数组）的转置，这种操作可通过 numpy.transpose 函数、ndarray.transpose 方法和 ndarray.T 特征属性实现，这三者是等同的。

import numpy as np
b = np.array([[ 0,  1,  2,  3],
              [10, 11, 12, 13],
              [20, 21, 22, 23],
              [30, 31, 32, 33],
              [40, 41, 42, 43]])

print(np.transpose(b))
print(b.T)
print(b.transpose())
# 以上三行均打印：
# [[ 0 10 20 30 40]
#  [ 1 11 21 31 41]
#  [ 2 12 22 32 42]
#  [ 3 13 23 33 43]]

3.1 改变数组的形状

import numpy as np

a = np.array([[ 0,  1,  2,  3],
              [10, 11, 12, 13],
              [20, 21, 22, 23]])

print(a.ravel())  # [ 0  1  2  3 10 11 12 13 20 21 22 23]

print(a.reshape(2, 6))
print(np.reshape(a, (2, 6)))
print(a.reshape(2, -1))
print(a.reshape(-1, 6))
# 以上 4 行代码均打印：
# [[ 0  1  2  3 10 11]
#  [12 13 20 21 22 23]]

3.1 改变数组的形状

最后介绍 numpy.resize 函数和ndarray.resize 方法。

numpy.resize 函数返回一个具有指定形状的新数组。不同于 reshape，resize 中给定的形状可以和原数组不兼容（元素数比原数组小或大），如果新给定的形状大于原数组，则新数组将以原数组的内容重复进行填充。该函数不影响原数组。

ndarray.resize 方法并不与 numpy.resize 等价，该方法将直接改变数组的形状和大小（在需要时重新为数组分配内存空间），并且当新形状大于原形状时，多出来的元素将以 0 填充（不是用原数组的内容重复填充）。

numpy.resize(a, new_shape)
ndarray.resize(new_shape, refcheck=True)

3.1 改变数组的形状

import numpy as np
a = np.array([[ 0,  1,  2,  3],
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])

print(np.resize(a, (3, 2)))
# [[0 1]
#  [2 3]
#  [4 5]]
print(np.resize(a, (3, 5)))
# [[ 0  1  2  3  4]
#  [ 5  6  7  8  9]
#  [10 11  0  1  2]]
# 这时 a 并没有改变

a.resize((3, 2))
print(a)
# [[0 1]
#  [2 3]
#  [4 5]]
a.resize(3, 4)
print(a)
# [[0 1 2 3]
#  [4 5 0 0]
#  [0 0 0 0]]

3.2 将不同数组堆叠在一起

多个数组可以沿不同的轴堆叠在一起。常用的函数包括：

• concatenate：沿现有轴连接一系列数组。
• stack：沿一个新的轴连接一系列数组。
• block：从嵌套的块列表中组装一个n 维数组。
• hstack：在水平方向（按列）堆叠数组。
• vstack：在垂直方向（按行）堆叠数组。
• dstack：按深度顺序堆叠数组(沿第三个轴)。
• column_stack：将一维数组作为列堆叠成二维数组。

3.2 将不同数组堆叠在一起

以下是使用 hstack 和 vstack 函数进行数组堆叠的示例：

import numpy as np
rng = np.random.default_rng()
a = np.floor(10 * rng.random((2, 2)))
print(a)
# [[4. 9.]
#  [2. 4.]]
b = np.floor(10 * rng.random((2, 2)))
print(b)
# [[5. 6.]
#  [0. 8.]]
print(np.vstack((a, b)))
# [[4. 9.]
#  [2. 4.]
#  [5. 6.]
#  [0. 8.]]
print(np.hstack((a, b)))
# [[4. 9. 5. 6.]
#  [2. 4. 0. 8.]]

3.3 将一个数组拆分成几个较小的数组

与堆叠相反，也可拆分数组。常用的函数包括：

• split：将一个数组拆分成多个相同大小的子数组，这些子数组都是原数组的视图。当不能等分时，将触发异常。
• array_split：与 split 相似，但不能等分时不会触发异常。
• hsplit：将一个数组水平（按列）拆分成多个相同大小的子数组。
• vsplit：将一个数组水平（按行）拆分成多个相同大小的子数组。
• dsplit：将一个数组沿第三轴（深度）拆分成多个相同大小的子数组。

3.3 将一个数组拆分成几个较小的数组

以下是使用 hsplit 函数进行数组拆分的示例：

import numpy as np
rng = np.random.default_rng()
a = np.floor(10 * rng.random((2, 12)))
print(a)
# [[5. 2. 5. 2. 8. 4. 9. 4. 6. 3. 3. 0.]
#  [6. 8. 0. 0. 9. 4. 4. 0. 0. 3. 9. 5.]]
print(np.hsplit(a, 3))
# [array([[5., 2., 5., 2.],
#        [6., 8., 0., 0.]]), array([[8., 4., 9., 4.],
#        [9., 4., 4., 0.]]), array([[6., 3., 3., 0.],
#        [0., 3., 9., 5.]])]
print(np.hsplit(a, (3, 4)))
# [array([[5., 2., 5.],
#        [6., 8., 0.]]), array([[2.],
#        [0.]]), array([[8., 4., 9., 4., 6., 3., 3., 0.],
#        [9., 4., 4., 0., 0., 3., 9., 5.]])]

4. 拷贝和视图

当对数据进行操作时，他们都数据有时被拷贝到一个新的数据，有时则没有。初学者经常会对此感到困惑。以下分三种情况介绍：

4.1 不拷贝

简单的赋值语句将不会拷贝对象和其中的数据。

Python 将可变对象作为引用传递，因此对这类对象，函数调用将不进行拷贝。

4.1 不拷贝

import numpy as np

a = np.array([[ 0,  1,  2,  3],
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])
b = a  # 没有创建新对象
print(b is a)  # True, a 和 b 是指向同一 ndarray 对象的两个名字

def f(x):
    print(id(x))

# 以下两个两行在每次调用时打印相同的值，但具体值则不固定
print(id(a))  # 4379335184
f(a)          # 4379335184

4.2 视图或浅拷贝

不同的数组对象可能共享相同的数据。view 方法创建一个新的数据对象，但和原数据共享相同的数据。

import numpy as np
a = np.array([[ 0,  1,  2,  3],
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])
c = a.view()
print(c is a)  # False
print(c.base is a)  # True,  c 是 a 所拥有的数据的一个视图
print(c.flags.owndata)  # False
c = c.reshape((2, 6))  # 改变 c 的形状并不会改变 a 的形状
print(a)
c[0, 4] = 1234  # 改变 c 的数据将同时改变 a 的数据
print(a)
# [[   0    1    2    3]
#  [1234    5    6    7]
#  [   8    9   10   11]]

4.2 视图或浅拷贝

切分一个数据将会返回它的一个视图。

import numpy as np

a = np.array([[ 0,  1,  2,  3],
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])
s = a[:, 1:3]
s[:] = 10  # s[:] 是 s 的一个视图。注意 s = 10 和 s[:] = 10 是不同的
print(a)
# [[ 0 10 10  3]
#  [ 4 10 10  7]
#  [ 8 10 10 11]]

4.3 深拷贝

copy 是对数据及其数据的全面拷贝，被成为深拷贝。

import numpy as np

a = np.array([[ 0,  1,  2,  3],
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])
d = a.copy()  # 创建一个新的具有独立数据的数据
print(d is a)  # False
print(d.base is a)  # False, d 和 a 不共享任何东西
d[0, 0] = 9999
print(a)  # a 还是原来的 a
# [[ 0  1  2  3]
#  [ 4  5  6  7]
#  [ 8  9 10 11]]

4.3 深拷贝

有时在进行切分后，如果原数据已经不再需要，则有必要调用一次 copy。例如，假设 a 是一个巨型的中间结果，而最终结果 b 仅包含 a 的一小部分，那么在通过切分得到 b 后应对其执行一次深拷贝：

import numpy as np
a = np.arange(int(1e8))
b = a[:100].copy()
del a  # 释放 a 所占用的内存

要是在以上代码中使用 b = a[:100]，那么 a 被 a，即便调用了 del a，其所占用的内存仍不会释放。

5. 广播

广播描述了 NumPy 如何在算术运算时处理具有不同形状数组的方式，从而使通用函数以直白的方式处理形状不完全相同的输入。在受规则约束的前提下，较小的数组在较大的数组上“广播”，以便它们具有兼容的形状。

NumPy 操作通常是在一对数组上逐元素进行。在最简单的情况下，两个数组必须具有完全相同的形状，如下所示：

import numpy as np

a = np.array([1., 2., 3.])
b = np.array([2., 2., 2.])
print(a * b)  # [2. 4. 6.]

5. 广播

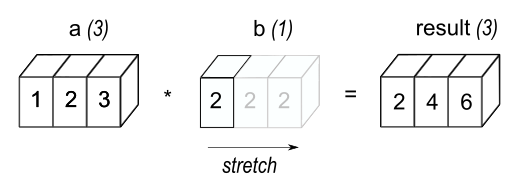
当数组的形状满足某些条件时，NumPy 的广播规则放宽了形状约束。如一个数组和一个标量值的操作组合，会发生最简单的广播示例：

import numpy as np

a = np.array([1., 2., 3.])
b = 2.0
print(a * b)  # [2. 4. 6.]

这里如同标量 b 被拉伸为和 a 形状相同的数组（NumPy 足够聪明，实际并没有发生拉伸）。

5. 广播

当对两个数组进行运算时，理想情况是这两个数组的形状完全相同（维度数相同，各维度也相同；或者说形状元组的元素个数相同，各元素值也相同）。广播机制使得即便达不到理想情况，也能进行运算。针对维度数不同和各维度不同，分别有两条规则：

1. 当两个数组的维度数不同时，对于较小维度数的数组，会在形状元组的左侧反复为缺失的维度补充 1，直到所有数组具有相同数量的维度。
2. 若数组的某维度为 1，而另一数组对应的维度大于 1，则该数组元素的值会进行广播，表现为具有沿该维度最大形状的数组的大小，且各元素值重复多次。

5. 广播

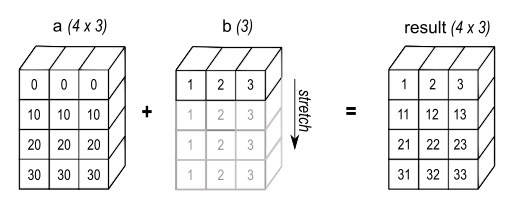
以上的两个规则不太容易理解，这里举例说明。对于如下两个数组 a 和 b，他们的形状分别为 (4, 3) 和 (3)。

a = np.array([[ 0.0,  0.0,  0.0],
              [10.0, 10.0, 10.0],
              [20.0, 20.0, 20.0],
              [30.0, 30.0, 30.0]])
b = np.array([1.0, 2.0, 3.0])
print(a + b)
# [[ 1.  2.  3.]
#  [11. 12. 13.]
#  [21. 22. 23.]
#  [31. 32. 33.]]
        

根据第 1 条规则，会把数组 b 的形状看作是 (1, 3)，即其值由 [1.0, 2.0, 3.0] 变为 [[1.0 2.0 3.0]]，这样两个数组将具有相同的维度数。

5. 广播

根据第 2 条规则，会进一步把形状 (1, 3) 中的维度 1 拉伸为 4，即将该维度对应的唯一元素 [1.0 2.0 3.0] 重复 4 次，相当于数组 b 变为：

[[1.0 2.0 3.0]
 [1.0 2.0 3.0]
 [1.0 2.0 3.0]
 [1.0 2.0 3.0]]
        

这样数组 a 和 b 就能进行运算了。下图为运算过程示意图。

5. 广播

关于两个或更多个数组是否能根据以上规则进行运算，可简单地把这些数组的形状放在一起，按照从右到左的顺序比较每一维度，缺失的元素不参与比较，当所有参与比较的元素值都满足如下条件时，就表示他们的维度是匹配的，或者说他们是可广播的：

1. 两个维度相等（即实现了精确匹配）；
2. 其中一个维度为 1（即维度 1 可以和任何维度相匹配）。

若不满足这两个条件，在运算时会抛出一个特定的异常，表明这参与运算的数组的形状不匹配。

5. 广播

根据此方法，可快速得出以下数组是可广播的：

A      (2d array):  5 x 4
B      (1d array):      1
Result (2d array):  5 x 4

A      (2d array):  5 x 4
B      (1d array):      4
Result (2d array):  5 x 4

A      (3d array):  15 x 3 x 5
B      (3d array):  15 x 1 x 5
Result (3d array):  15 x 3 x 5

A      (3d array):  15 x 3 x 5
B      (2d array):       3 x 5
Result (3d array):  15 x 3 x 5

A      (3d array):  15 x 3 x 5
B      (2d array):       3 x 1
Result (3d array):  15 x 3 x 5
        

5. 广播

以下数组是不可广播的：

A      (1d array):  3
B      (1d array):  4 # 最后的维度不匹配

A      (2d array):      2 x 1
B      (3d array):  8 x 4 x 3 # 倒数第二个维度不匹配
        

6. 高级索引和索引技巧

相比于常规的 Python 序列，NumPy 提供了更多了索引功能。除了前面看到的通过整数和切片索引，还可以通过整数数组和布尔数组对数组进行索引。

6.1 使用索引数组进行索引

import numpy as np

a = np.arange(12)**2  # 最前面的 12 个平方数
i = np.array([1, 1, 3, 8, 5])  # 一个索引数组
print(a[i])  # [ 1  1  9 64 25]，数组 a 在位置 i 处的元素
j = np.array([[3, 4], [9, 7]])  # 二维的索引数组
print(a[j])  # 结果数组的形状与 j 相同
# [[ 9 16]
#  [81 49]]

6.1 使用索引数组进行索引

当被索引数组 a 为多维时，单个索引数组将引用 a 的第一维。以下示例通过使用调色板将将一个标签图像转换为一个实际的颜色图像。

import numpy as np

palette = np.array([[0, 0, 0],         # 黑色
                    [255, 0, 0],       # 红色
                    [0, 255, 0],       # 绿色
                    [0, 0, 255],       # 蓝色
                    [255, 255, 255]])  # 白色
image = np.array([[0, 1, 2, 0],   # 每个值对应调色板中的一个颜色
                  [0, 3, 4, 0]])  # 一个包含 2*4 个像素的图像
print(palette[image])  # (2, 4, 3) 颜色图像
# [[[  0   0   0]
#   [255   0   0]
#   [  0 255   0]
#   [  0   0   0]]

#  [[  0   0   0]
#   [  0   0 255]
#   [255 255 255]
#   [  0   0   0]]]

6.1 使用索引数组进行索引

我们还可以给定超过一维的索引。每一维度的索引数组应具有相同的形状。

import numpy as np
a = np.arange(12).reshape(3, 4)
print(a)
# [[ 0  1  2  3]
#  [ 4  5  6  7]
#  [ 8  9 10 11]]
i = np.array([[0, 1],  # 数组 a 的第一维索引
              [1, 2]])
j = np.array([[2, 1],  # 第二维索引
              [3, 3]])
print(a[i, j])  # i 和 j 必须具有相同的形状
# [[ 2  5]
#  [ 7 11]]
print(a[i, 2])
# [[ 2  6]
#  [ 6 10]]
print(a[:, j])
# [[[ 2  1]
#   [ 3  3]]

#  [[ 6  5]
#   [ 7  7]]

#  [[10  9]
#   [11 11]]]

6.1 使用索引数组进行索引

在 Python 中，arr[i, j] 和 arr[(i, j)] 几乎是完全等同的，因此我们可以将 i 和 j 放入一个元组中，并使用如下方法进行索引。

import numpy as np
a = np.arange(12).reshape(3, 4)
print(a)
# [[ 0  1  2  3]
#  [ 4  5  6  7]
#  [ 8  9 10 11]]
i = np.array([[0, 1],  # 数组 a 的第一维索引
                [1, 2]])
j = np.array([[2, 1],  # 第二维索引
                [3, 3]])
l = (i, j)  # 等同于 a[i, j]
print(a[l])
# [[ 2  5]
#  [ 7 11]]

6.1 使用索引数组进行索引

不过，我们并不能把 i 和 j 放进一个数组中，因为这个数组将被解释维对 a 的第一维数据的索引。

import numpy as np
a = np.arange(12).reshape(3, 4)
print(a)
# [[ 0  1  2  3]
#  [ 4  5  6  7]
#  [ 8  9 10 11]]
i = np.array([[0, 1],  # 数组 a 的第一维索引
                [1, 2]])
j = np.array([[2, 1],  # 第二维索引
                [3, 3]])
s = np.array([i, j])
# 不是我们想要的
# print(a[s])  # IndexError: index 3 is out of bounds for axis 0 with size 3
print(a[tuple(s)])  # 与 a[i, j] 相同
# [[ 2  5]
#  [ 7 11]]

6.1 使用索引数组进行索引

另一个使用数组进行索引的常见用法是搜索时间相关数据序列的最大值：

import numpy as np
time = np.linspace(20, 145, 5)  # 时间标度
data = np.sin(np.arange(20)).reshape(5, 4)  # 4 组时间相关数据
print(time)  # [ 20.    51.25  82.5  113.75 145.  ]
print(data)
# [[ 0.          0.84147098  0.90929743  0.14112001]
#  [-0.7568025  -0.95892427 -0.2794155   0.6569866 ]
#  [ 0.98935825  0.41211849 -0.54402111 -0.99999021]
#  [-0.53657292  0.42016704  0.99060736  0.65028784]
#  [-0.28790332 -0.96139749 -0.75098725  0.14987721]]
ind = data.argmax(axis=0)  # 每组数据的最大值的索引
print(ind)  # [2 0 3 1]
time_max = time[ind]  # 最大值对应的时间
data_max = data[ind, range(data.shape[1])]  # => data[ind[0], 0], data[ind[1], 1]...
print(time_max)  # [ 82.5   20.   113.75  51.25]
print(data_max)  # [0.98935825 0.84147098 0.99060736 0.6569866 ]
print(np.all(data_max == data.max(axis=0)))  # True

7. 输入和输出

使用 NumPy 处理数据时，经常遇到需要从其他来源（一般对应不同格式的文件）输入数据进行处理，以及把经处理后的数据输出为各种格式的文件的情况。这些工作有时候很简单，如以规整的文本文件输入或输出；有时却非常复杂，如需要对数据异常或缺失的情况进行判断，需要输入或输出为其他复杂的格式，如 Excel、SQL、JSON、Parquet、HTML、HDF5，等等。

对于相对较简单的输入和输出，NumPy 自身提供了部分输入和输出函数可胜任此项工作。对于复杂的输入和输出，则需要借助其他软件库，如著名的 pandas。

本节仅介绍 NumPy 自身的输入输出功能，如果这些已不能满足您的要求，请进一步学习 pandas 一章的内容。

7.1 以二进制文件保存和加载

把 NumPy 数组以文件的形式保存的最快捷、最精确的方法是 save、savez 和 savez_compressed 系列函数。他们的签名如下：

numpy.save(file, arr, allow_pickle=True, fix_imports=True)
numpy.savez(file, *args, **kwds)
numpy.savez_compressed(file, *args, **kwds)

他们都保存为二进制文件（非文本文件，由字节序列而非字符序列构成，如果用文本编辑器打开，一般显示乱码）。区别是：

• save 将单个数组保存为 .npy 后缀格式的 NumPy 特有二进制文件；
• savez 将多个数组保存为未压缩的 .npz 后缀格式的 NumPy 特有的单个二进制文件；
• savez_compressed 将多个数组保存为压缩的 .npz 后缀格式的 NumPy 特有的单个二进制文件。

7.1 以二进制文件保存和加载

import numpy as np

a = np.arange(10).reshape(2, 5)
b = a * 2
np.save('array_a.npy', a)
np.savez('array_a_b.npz', a, b)
np.savez_compressed('array_a_b_compressed.npz', a, b)

注意：以上代码中，各个文件名都没有给出完整的路径，你可能不知道文件被保存到哪里了。其实他们都被保存到当前工作目录中了。如果你是从 VS Code 运行代码，并且只是打开一个源文件运行代码，那么当前工作目录一般是你操作系统的用户根目录；如果你用 VS Code 打开了一个目录（项目），则该目录就是工作目录。你可以使用 os.getcwd 查看当前工作目录，也可以使用 os.chdir 更改当前工作目录。

7.1 以二进制文件保存和加载

要将以上保存的二进制文件恢复回来，需要使用 load 函数。

numpy.load(file, mmap_mode=None, allow_pickle=False, fix_imports=True,
           encoding='ASCII', *, max_header_size=10000)

对于 .npy 文件，load 函数直接返回一个数组对象：

import numpy as np

a = np.arange(10).reshape(2, 5)
np.save('array_a.npy', a)
b = np.load('array_a.npy')
print(b)
# [[0 1 2 3 4]
#  [5 6 7 8 9]]

7.1 以二进制文件保存和加载

当用 .npz 文件保存和恢复多个数组时，情况有点复杂。默认 savez 和 savez_compressed 函数并不保存数组变量的名称，而是自动给其赋予类似 arr_0、arr_1 的名称。同时 load 返回的是 NpzFile 对象，其中包含类似 {filename: array} 键值对形式的字典，可以通过其 files 属性查看其中包含的数组。

import numpy as np
a = np.arange(10).reshape(2, 5)
b = np.sin(a)
np.savez('array_a_b.npz', a, b)  # a, b 会被匹配到 *args 参数对应的元组值
npz = np.load('array_a_b.npz')
print(npz.files)  # ['arr_0', 'arr_1']
print(npz['arr_0'])  # 数组 a 的值
print(npz['arr_1'])  # 数组 b 的值
npz.close()  # 最终需要关闭此 NpzFile 文件

7.1 以二进制文件保存和加载

也可以不使用 savez 和 savez_compressed 函数的位置参数 *args，而使用其关键字参数 **kwds 显式指定各数组的保存名称：

import numpy as np
a = np.arange(10).reshape(2, 5)
b = np.sin(a)
np.savez('array_a_b.npz', a=a, b=b)  # a=a, b=b 被匹配到关键字参数 **kwds
npz = np.load('array_a_b.npz')
print(npz.files)  # ['a', 'b']
print(npz['a'])  # 数组 a 的值
print(npz['b'])  # 数组 b 的值
npz.close()  # 最终需要关闭此 NpzFile 文件

7.2 以文本文件保存和加载

以上使用二进制文件的一个明显缺点是只能使用 NumPy 加载文件，如果希望从其他源导入数据，或者将数据导出给其他程序使用，最简单的方法是将其保存为文本文件。这需要使用 savetxt 和 loadtxt 函数，他们一次只能操作一个数组。

numpy.savetxt(fname, X, fmt='%.18e', delimiter=' ', newline='\n',
              header='', footer='', comments='# ', encoding=None)

numpy.loadtxt(fname, dtype=<class 'float'>, comments='#', delimiter=None,
converters=None, skiprows=0, usecols=None, unpack=False, ndmin=0,
encoding='bytes', max_rows=None, *, quotechar=None, like=None)

可以通过 fmt 指定元素值的输出格式，通过 header、footer 和 delimiter 为文本文件指定页眉、页脚和不同的分隔符，不过要记得保存和加载文件时使用相同的 delimiter。

7.2 以文本文件保存和加载

一个示例：

import numpy as np

a = np.arange(10).reshape(2, 5)
np.savetxt('array_a.csv', a)
b= np.loadtxt('array_a.csv')
print(b)
# [[0. 1. 2. 3. 4.]
#  [5. 6. 7. 8. 9.]]

可以看出，按默认方式保存为文本文件再加载回来后，数据是有损耗的，原来数组中存储的是整数，保存时却变为浮点数，加载回来后也是浮点数。

7.2 以文本文件保存和加载

当用文本文件交换数据时，经常使用 .csv 格式的文本文件，其名称是逗号分割值（Comma-Separated Values）文件。不过数据元素之间不一定总是使用逗号分割，因此也称为字符分割值文件。对于上页中保存的文件，其内容为：

0.000000000000000000e+00 1.000000000000000000e+00 2.000000000000000000e+00 3.000000000000000000e+00 4.000000000000000000e+00
5.000000000000000000e+00 6.000000000000000000e+00 7.000000000000000000e+00 8.000000000000000000e+00 9.000000000000000000e+00

savetxt 函数在保存数组时，默认使用空格作为分隔符，不过也可以通过 delimiter 关键字参数指定其他分隔符。常用的分割符包括空格 ' '、水平制表符 '\t'、逗号 ',' 和分号 ';'。另外，使用电子表格程序，如 Excel、WPS 表格一般能很方便地导入、导出和编辑此种格式的文件。

7.3 使用 genfromtxt 函数导入

以上 loadtxt 函数的功能较弱。例如，当文件中某个值缺失时，当需要分别指定各列的数据类型时，当仅需选择多列中的特定列时，当就无法应对。这时就需要使用 genfromtxt，这是一个更加强大和复杂的函数。该函数有很多参数：

numpy.genfromtxt(fname, dtype=<class 'float'>, comments='#',
delimiter=None, skip_header=0, skip_footer=0, converters=None,
missing_values=None, filling_values=None, usecols=None, names=None,
excludelist=None, deletechars=" !#$%&'()*+, -./:;<=>?@[\\]^{|}~",
replace_space='_', autostrip=False, case_sensitive=True, defaultfmt='f%i',
unpack=None, usemask=False, loose=True, invalid_raise=True, max_rows=None,
encoding='bytes', *, ndmin=0, like=None)

所以，请做好心理准备，掌握该函数需要花一番功夫。

7.3 使用 genfromtxt 函数导入

genfromtxt 唯一必须提供的参数是第一个 fname，该参数可以是：

• 单个字符串。这时会将该字符串当作本地或远程文件的名称。该字符串甚至可以是一个 URL 或远程文件，这时会自动下载文件到当前工作目录并打开。
• 一个字符串的列表。这时会将整个列表看作文件内容，每个字符串被当作文件中的一行。
• 一个生成器或类似文件的对象。该对象必须实现了 read 方法，如一个文件对象，或一个 io.StringIO 对象。

当加载文件时，文件既可以是文本文件，也可以是文本文件的压缩存档文件。目前支持的压缩类型包括 gzip 压缩（具有后缀 .gz）和 bzip2 压缩（后缀 .bz2）。

7.3 使用 genfromtxt 函数导入

一个简单的示例：

import numpy as np
# s 是字符串列表, 各个值以逗号分割,
# 注意列表的第一个元素长度少于第二个元素
s = ['0,1,2,3,', '5,6,7,8,9']
a = np.genfromtxt(s, delimiter=",")
print(a)
# [[ 0.  1.  2.  3. nan]
#  [ 5.  6.  7.  8.  9.]]
# 按照默认, 原来的整数类型仍然被转换为浮点类型了,
# 不过它能处理缺失的元素了, nan 代表非数字

作业

作业

要求：

1. 将本章全部作业放在一个 安模作业03-01-学号-姓名.py 的源文件中，通过电子邮件以附件形式发给任课教师。
2. 在源文件中以注释的形式醒目地写明本次作业对应的章编号、各个作业题的编号，并按要求写出解题思路、代码注释。
3. 以上各题不能只有文字说明，而应同时有可执行的示例代码。
4. 邮件标题统一用 安模作业03-01-学号-姓名 的形式。
5. 所有关于作业的回答都以代码注释的形式写在源文件中，不需要再额外附加其他文档或图片，请保证代码执行不会发生错误。
6. 待本次作业批改后，请通过此链接下载本次作业的参考答案。