安全工程专业课程
安全仿真与模拟基础
金洪伟 & 闫振国 & 王延平
西安科技大学安全科学与工程学院
如何浏览?
- 从浏览器地址栏打开 https://zimo.net/aqmn/;
- 点击章节列表中的任一链接,打开相应的演示文稿;
- 点击链接打开演示文稿,使用空格键或方向键导航;
- 按f键进入全屏播放,再按Esc键退出全屏;
- 按Alt键同时点击鼠标左键进行局部缩放;
- 按Esc或o键进入幻灯片浏览视图。
请使用最新版本浏览器访问此演示文稿以获得更好体验。
第 3 部分 基于 Python 进行科学计算
第 5 章 SymPy
计算机代数系统
目 录
1. 快速入门
1.1 SymPy 介绍

SymPy 是一个用于符号数学的 Python 库。其目标是成为一个全功能的计算机代数系统,同时保持代码的简单性,使其可理解和易扩展。SymPy 完全由 Python 编写。
计算机代数(Computer Algebra)又称符号计算(Symbolic Computation),它是与数值计算(Numerical Computation)相对的概念,对“符号”的运算代替了对“数”的运算。符号可以代表整数、有理数、实数和复数,也可以代表多项式、函数,还可以代表数学结构,如集合、群、环、代数等等。
计算机代数系统(Computer Algebra System)又称符号代数系统(Symbolic Algebra System),是一种数学软件,它能像传统的用纸和笔手工进行数学运算、公式推导那样处理数学表达式。
1.1 SymPy 介绍
SymPy 的特征:
- 开源且免费:SymPy 在 BSD 开源协议下发布,它是自由且免费的。
- 与 Python 完美契合:SymPy 完全由 Python 编写,且完全通过 Python 程序执行。这不像其他计算机代数系统往往需要发明一个简陋的语言。如果你已经掌握 Python,将很快能掌握 SymPy。
- 轻量级:相对于其他计算机代数系统,SymPy 的尺寸非常小,仅依赖 Python 即可运行。这意味着它很容易被安装,且能在各种环境中运行。
- SymPy 可作为库运行:其他计算机代数系统主要关注在交互式环境中的可用性,很难被扩展或用于自动化处理。而 SymPy 同样可用于 Python 的交互式环境,同时可被用于你自己的 Python 程序中。
1.2 安装
使用 pip 安装:
$ pip install sympy使用 conda安装:
conda install numpy如果你使用 Python 的 Anaconda 发行版,则 SymPy 已经被包含在其中,不需再进行安装。更多的安装方法请见此页。
1.3 符号计算的特点
以下程序展示了符号计算和数值计算的区别:
import math
import sympy
print(math.sqrt(4)) # 2.0
print(sympy.sqrt(4)) # 2
print(math.sqrt(2)) # 1.4142135623730951
print(sympy.sqrt(2)) # sqrt(2)
print(math.sqrt(8)) # 2.8284271247461903
print(sympy.sqrt(8)) # 2*sqrt(2)对于符号计算系统,在计算非完全平方数(如 3, 5, 6, 7, 8)的平方根时,其结果是无理数,这时默认将以未求值的形式给出结果。
1.4 符号变量和符号表达式
符号计算的主要特征是通过符号变量对符号表达式进行计算。在 SymPy 中,符号变量就是普通的 Python 变量,它同样必须先定义,再使用(这与其他计算机代数系统不同)。可通过 symbols 函数定义符号变量。
from sympy import symbols
a, b, c, x = symbols("a b c x")
y = 2*a*x**2 + 3*b*x
y += 4*b*x + c
print(y) # 2*a*x**2 + 7*b*x + csymbols 函数接受一个字符串,字符串中各个变量以空格或逗号分割,字符串中的变量名和赋值的等号前面的变量名一般相同,但也可不同。
1.4 符号变量和符号表达式
在其他计算机代数系统中,公式表达式 $4x$ 可能写作 4x 或 4 x,但在 SymPy 中,却必须写作 4*x。这是因为符号变量的运算必须符合 Python 的语法,这让熟悉 Python 的人,不需要太多学习就能编写正确的符号表达式。
在其他系统中,求幂(指数运算)一般使用脱字符 ^,但在 Python 中则使用 **,SymPy 同样遵循后者的规则,因此 $x^2$ 应该写成 x**2 而不是 x^2,而 ^ 仍然是位运算符,表示按位异或。
1.4 符号变量和符号表达式
我们以往用 Python 进行编程时,所操作的都是 Python 对象。在本章中,仿佛进入一个新世界,这里所操作的主要是 SymPy 对象。当用常规的操作符对两个对象进行操作时,只要其中有一个 SymPy 对象,结果将是 SymPy 对象。
from sympy import *
y = 1 + 1
print(y, type(y)) # 2 <class 'int'>
y = Integer(1) + 1
print(y, type(y)) # 2 <class 'sympy.core.numbers.Integer'>
y = Float(1) + 1
print(y, type(y)) # 2.00000000000000 <class 'sympy.core.numbers.Float'>
y = Integer(1) + 1.0
print(y, type(y)) # 2.00000000000000 <class 'sympy.core.numbers.Float'>1.4 符号变量和符号表达式
在符号计算中,有理数 $\frac{1}{2}$ 通常不应该被表示为 0.5,而有理数 $\frac{1}{3}$ 更不应该表示为其近似值 0.3333333333333333。然而,Python 默认会计算两个整数的比值,即他们默认是 Python 对象而不是 SymPy 对象。
为了产生有理数形式的 SymPy 对象,可以强制将整数的除法运算的分子、分母或两者同时转换为 SymPy 对象;也可以使用 Rational 类直接生成有理数。
from sympy import *
x = Integer(1) / 2
print(x, type(x)) # 1/2 <class 'sympy.core.numbers.Half'>
x = 1 / Integer(3)
print(x, type(x)) # 1/3 <class 'sympy.core.numbers.Rational'>
x = Integer(1) / Integer(3)
print(x, type(x)) # 1/3 <class 'sympy.core.numbers.Rational'>
x = Rational(1, 2)
print(x, type(x)) # 1/2 <class 'sympy.core.numbers.Half'>1.4 符号变量和符号表达式
在 Python 中,单个等号 = 是赋值运算符,两个等号 == 是判断两个表达式是否相等的比较运算符,后者的结果总是 True 或 False,那么该如何表达数学中的等式呢?这就需要用到 SymPy 中的 Eq 对象(它是 Equality 的别名)。
例如,对于等式 $3x^2=4x-2$ 可以写为 Eq(3*x**2, 4*x - 2),不能写成 3*x**2 = 4*x - 2 或 3*x**2 == 4*x - 2。以下代码实现了对该方程的求解:
from sympy import *
x = symbols('x')
print(solve(Eq(3*x**2, 4*x - 2), x))1.5 释放符号计算的威力
可使用 SymPy 来化简表达式、求导、积分、求极限、解方程、进行矩阵运算,等等。SymPy 还包括更多的模块,用来绘图、以美观的形式打印、输出为 $\LaTeX$ 格式、代码生成、物理学、统计学、组合数学、数论、几何学、逻辑学,等等。下面将简单地列举一些进行这种运算的示例。
在以下几页的示例中,都假设程序的开头几行代码为:
# 导入 sympy 模块中的所有项目,下面代码将不需加 sympy. 前缀
from sympy import *
x, y, z = symbols("x y z") # 在数学中最常用的变量名称1.5 释放符号计算的威力
一个更复杂的示例,该示例对多项式进行展开和因式分解:
from sympy import symbols, expand, factor
a, b, c, x = symbols("a, b, c, x")
y1 = 2*a*x**2 + 3*b*x
y2 = b*x + c
expr = y1 * y2
print('原始:', expr) # 原始: (2*a*x**2 + 3*b*x)*(b*x + c)
expanded_expr = expand(expr)
print('展开:', expanded_expr)
# 展开: 2*a*b*x**3 + 2*a*c*x**2 + 3*b**2*x**2 + 3*b*c*x
print('因式分解:', factor(expanded_expr))
# 因式分解: x*(2*a*x + 3*b)*(b*x + c)1.6 打印输出
虽然前面只是在命令行中以普通的字符串表达式的形式打印符号表达式,但 SymPy 也支持打印输出为其他公式格式,其主要支持的格式包括:str(默认)、srepr、pretty printer、LaTeX、MathML、Dot,可分别通过 str、srepr、pretty、latex、mathml、dotprint 函数将普通的表达式转换为这些格式。如下所示:
from sympy import *
s1, s2, s3 =symbols('sigma_1, sigma_2, sigma_3')
first_invariant = s1 + s2 + s3
print(first_invariant)
print(str(first_invariant))
print(pretty(first_invariant)) # 如果终端支持 Unicode,则自动使用 Unicode
print(pretty(first_invariant, use_unicode=True)) # 强制使用 Unicode
print(latex(first_invariant))
print(mathml(first_invariant))
print(dotprint(first_invariant))1.6 公式输出
在平时应用中,经常可以以 $\LaTeX$ 的形式输出结果,然后将其复制到 MathType 或 AxMath 等公式编辑器中,即可得到完美显示的公式。例如,将以上运算所得的 $\LaTeX$ 公式文本 \sigma_{1} + \sigma_{2} + \sigma_{3} 复制到公式编辑器中,其效果如下:
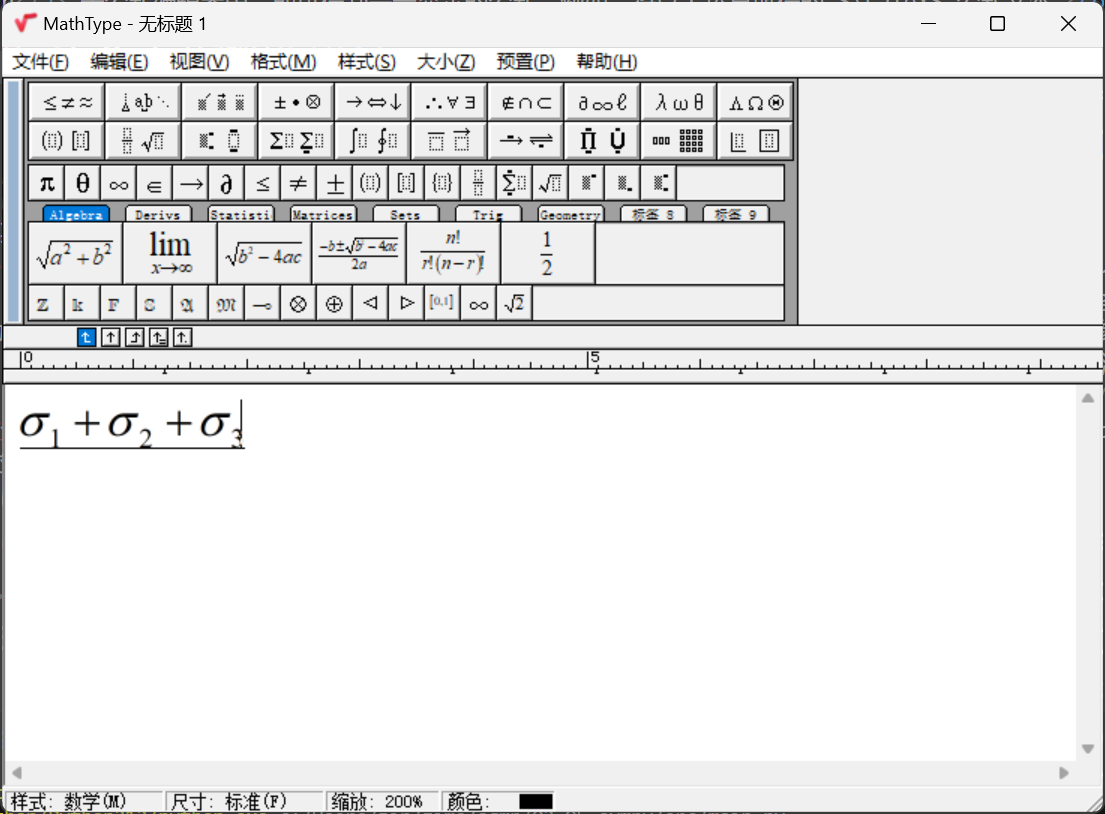
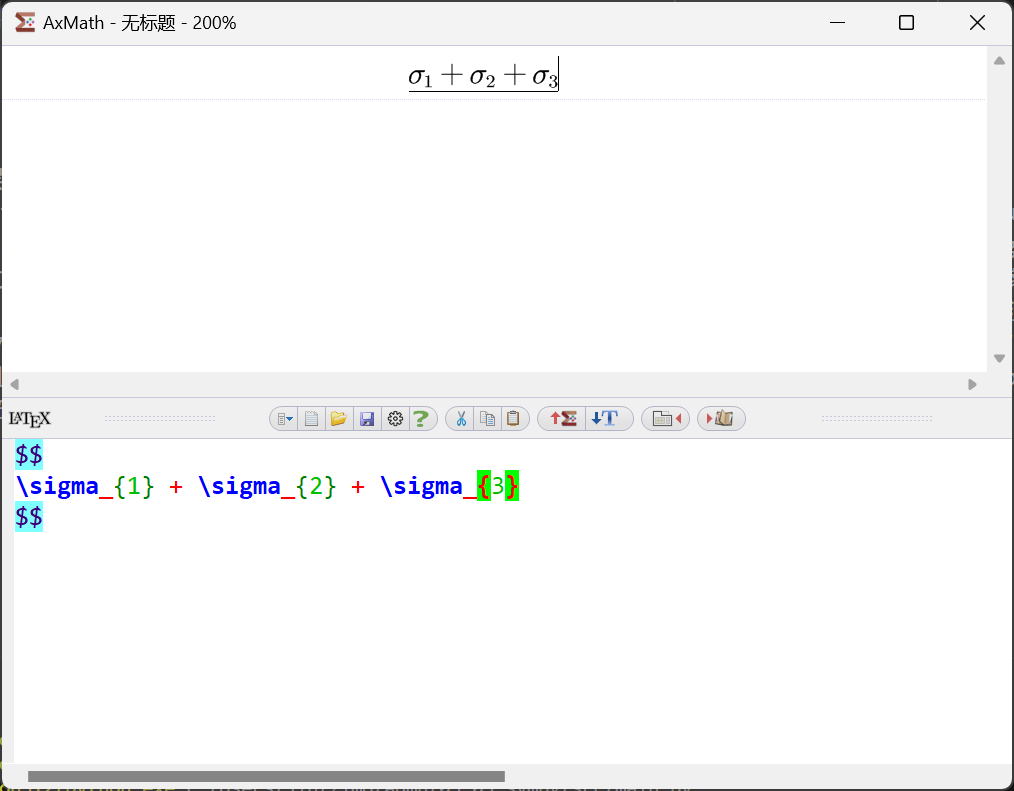
本页显示效果:
$$\sigma_{1} + \sigma_{2} + \sigma_{3}$$
1.7 应用示例
在考虑煤对瓦斯的动态吸附作用时,瓦斯在煤层中的达西渗流的控制方程为:
$$\frac{\partial}{\partial t}\left( \frac{abp}{1+bp}+\frac{\varphi T_np}{Tp_n} \right) -\frac{KT_n}{2\mu Tp_n}\left[ \frac{\partial ^2\left( p^2 \right)}{\partial x_{1}^{2}}+\frac{\partial ^2\left( p^2 \right)}{\partial x_{2}^{2}}+\frac{\partial ^2\left( p^2 \right)}{\partial x_{3}^{2}} \right] =0$$
式中,p 为瓦斯压力,a, b 为吸附常数,t 为时间,K 为渗透率,μ 为流体的动力粘度系数,x1, x2, x3 为三维坐标分量,T 为气体的热力学温度,Tn 为常温对应的热力学温度,Tn = 25 + 273.15 = 298.15K,pn 为 1 标准大气压,pn = 101325.0Pa。
在数值计算中,需要将该式转换为偏微分方程组的标准形式,即其中只包含 $\frac{\partial p}{\partial t}$, $\frac{\partial p}{\partial x}$ 和 $\frac{\partial ^2p}{\partial x^2}$ 这些偏导数项。该转换过程可以通过下页代码做到。
1.7 应用示例
K, mu, T, T_n = symbols('K mu T T_n')
a, b, varphi, p_n = symbols('a b varphi p_n')
p = symbols('p', cls=Function)
eq1 = diff((a*b*p(x1, x2, x3, t) / (1 + b*p(x1, x2, x3, t)) + varphi*T_n*p(x1, x2, x3, t)/(T*p_n)), t) - \
K*T_n/(2*mu*p_n*T) * (diff((p(x1, x2, x3, t)*p(x1, x2, x3, t)), x1, x1) + diff((p(x1, x2, x3, t)*p(x1, x2, x3, t)), x2, x2) + diff((p(x1, x2, x3, t)*p(x1, x2, x3, t)), x3, x3))
print('所得标准形式的公式为:\n', latex(eq1))将打印结果稍加整理,即可得到标准形式的公式为:
$$\left[ \frac{ab}{1+bp}-\frac{ab^2p}{\left( 1+bp \right) ^2}+\frac{\varphi T_n}{Tp_n} \right] \frac{\partial p}{\partial t}-\frac{KT_np}{\mu Tp_n}\left( \frac{\partial ^2p}{\partial x_{1}^{2}}+\frac{\partial ^2p}{\partial x_{2}^{2}}+\frac{\partial ^2p}{\partial x_{3}^{2}} \right) \newline -\frac{KT_n}{\mu Tp_n}\left[ \left( \frac{\partial p}{\partial x_1} \right) ^2+\left( \frac{\partial p}{\partial x_2} \right) ^2+\left( \frac{\partial p}{\partial x_3} \right) ^2 \right] =0$$
2. 基础操作
3. 打印
4. 化简
5. 微积分
6. 解方程
7. 矩阵运算
8. 高级的表达式操作
作业
作业
要求:
- 将本章全部作业放在一个
安模作业03-05-学号-姓名.py的源文件中,通过电子邮件以附件形式发给任课教师。 - 在源文件中以注释的形式醒目地写明本次作业对应的章编号、各个作业题的编号,并按要求写出解题思路、代码注释。
- 以上各题不能只有文字说明,而应同时有可执行的示例代码。
- 邮件标题统一用
安模作业03-05-学号-姓名的形式。 - 所有关于作业的回答都以代码注释的形式写在源文件中,不需要再额外附加其他文档或图片,请保证代码执行不会发生错误。
- 待本次作业批改后,请通过此链接下载本次作业的参考答案。