《安全仿真与模拟基础》课程设计

1 概述

在《安全仿真与模拟基础》课程教学过程中，我们初步学习了计算机程序设计的基础知识，并能通过编程开发解决一些简单的问题。为了进一步巩固所学知识，提高使用计算机技术解决工程问题的能力，此次课程设计将针对一个较复杂的工程问题，对其进行建模、模拟和分析。

具体来说，此次课程设计所要解决的工程问题是矿井通风网络解算问题，这是我们在《矿井通风》课程中所熟知的问题。这里推荐使用的编程语言是 Python，选用 Python 时，一般要同时使用著名的数学计算基础包 NumPy。另外，也可使用 MATLAB（或其开源替代 GNU Octave、Scilab）、Julia 或任何其他语言或工具对此问题进行模拟求解。

由于我们在学习本课程时并没有涉及到所有与此次课程设计相关的知识，加上矿井通风网络解算过程本身比较复杂，所以在此页面将较为详细地介绍通风网络解算的原理，所使用软件模块的简介、安装和使用，编程开发的基本思路和过程，如何使用所编写程序进行模拟，等等。请务必认真地阅读此文档！

2 设计目标、内容与要求

2.1 设计目标

  1. 提升学生应用计算机技术的能力，尤其是程序设计的能力，能通过程序设计解决一些初级的安全工程问题；
  2. 锻炼学生将所学知识应用于科研和工程实践的能力，加深对《安全仿真与模拟基础》、《矿井通风》等课程的理解；
  3. 掌握使用计算机技术对安全工程领域问题进行数值建模和模拟分析的基本方法和步骤，为毕业设计和将来科研、工作中对实际工程问题建模和解算奠定基础。

2.2 设计内容

  1. 矿井通风网络的数学建模。将矿井的巷道网络简化为图，用关联矩阵描述此图，并进一步以矩阵形式表示风量守恒定律、能量守恒定律和通风阻力定律，以此构成求解通风网络的方程组，并给出用牛顿法求解此方程组的原理和过程。
  2. 矿井通风网络的计算机建模和求解。基于特定的科学计算软件（如 Python + NumPy 或 MATLAB）对矿井通风网络进行数值建模和解算。
  3. 利用矿井通风网络解算程序解决一个实际工程问题。由学生根据网络文献自由选择一个工程问题进行建模和求解，常见的问题如通风网络解算，以及基于通风网络解算分析通风系统的稳定性。

2.3 时间和地点

2.4 要求

  1. 掌握对矿井通风网络进行数学建模的方法，能清晰解释所建立的矩阵形式方程组各参数的意义；能使用 Python（或是其他编程语言或工具）编制基本的通风网络解算程序，能对程序进行调整以适用不同的解算需求。
  2. 在课程设计结束时，每人提交一份课程设计报告打印稿，同时将电子稿（包括源代码）发送到任课教师的电子邮箱（jinhw@qq.com）；请统一使用此模板撰写课程设计报告，发送电子邮件时，邮件和附件标题统一为《安全仿真与模拟基础》课程设计-姓名-学号。
  3. 课程设计报告应做到逻辑清晰、计算和分析正确、没有重大遗漏、排版规范；所提交的代码应做到能正确运行、完成度高、逻辑清晰、可读性强、风格良好；学生应该清晰地口头阐述设计原理和思路。
  4. 报告和代码可以参照甚至借用此文档以及附带的代码，但同学见相互不能存在抄袭现象，一般提交的报告和代码越新颖（和本文档以及其他同学差异大），且不存在重大问题。
  5. 课程设计主要在教室完成，不缺勤、迟到和早退，积极和老师讨论问题。

2.5 更多建议

每个学生可根据自身特点将课程设计精力主要放在完善设计报告，完善附带的通风网络解算程序，或用此程序解决一个工程问题。请务必清晰地描述本次设计的亮点！

以下给出部分可在本文档及附带代码基础上可额外实施的工作方向：

  1. 针对一个具体的矿井通风系统，描述矿井通风系统的基本情况，画出其通风网络图，并进行数值建模和求解，对求解结果进行解释。
  2. 从网络学习程序流程图的绘制方法，绘制此通风网络解算程序的流程图。
  3. 为此程序编制根据风量—风压采样数据，自动使用最小二乘法拟合得到通风机特性曲线的代码。
  4. 用类重新实现本程序的功能，提高代码的模块化程度（建议核心类的名称为 MineVentilationNetwork）。
  5. 将所有的建模数据放在一个文件中（如 JSON 或 ini 文件），实现程序和建模数据的彻底分离。
  6. 对一些文献资料中的通风网络解算进行验证（如这篇），看看结果有没有差异，分析产生差异的原因。
  7. 用此通风网络解算程序对一些文献上讨论的风网（如较复杂的角联通风）进行解算分析，讨论这类风网的稳定性。
  8. 分析本文档给出的通风网络解算方法和课本上主要讨论的回路风量法的区别，以及各自的优缺点。
  9. 基于此次课程设计内容，针对通风网络解算、通风系统隐患识别、通风系统优化等研究领域，讨论自己的见解。

3 矿井通风网络的数学建模

3.1 用图表示通风网络

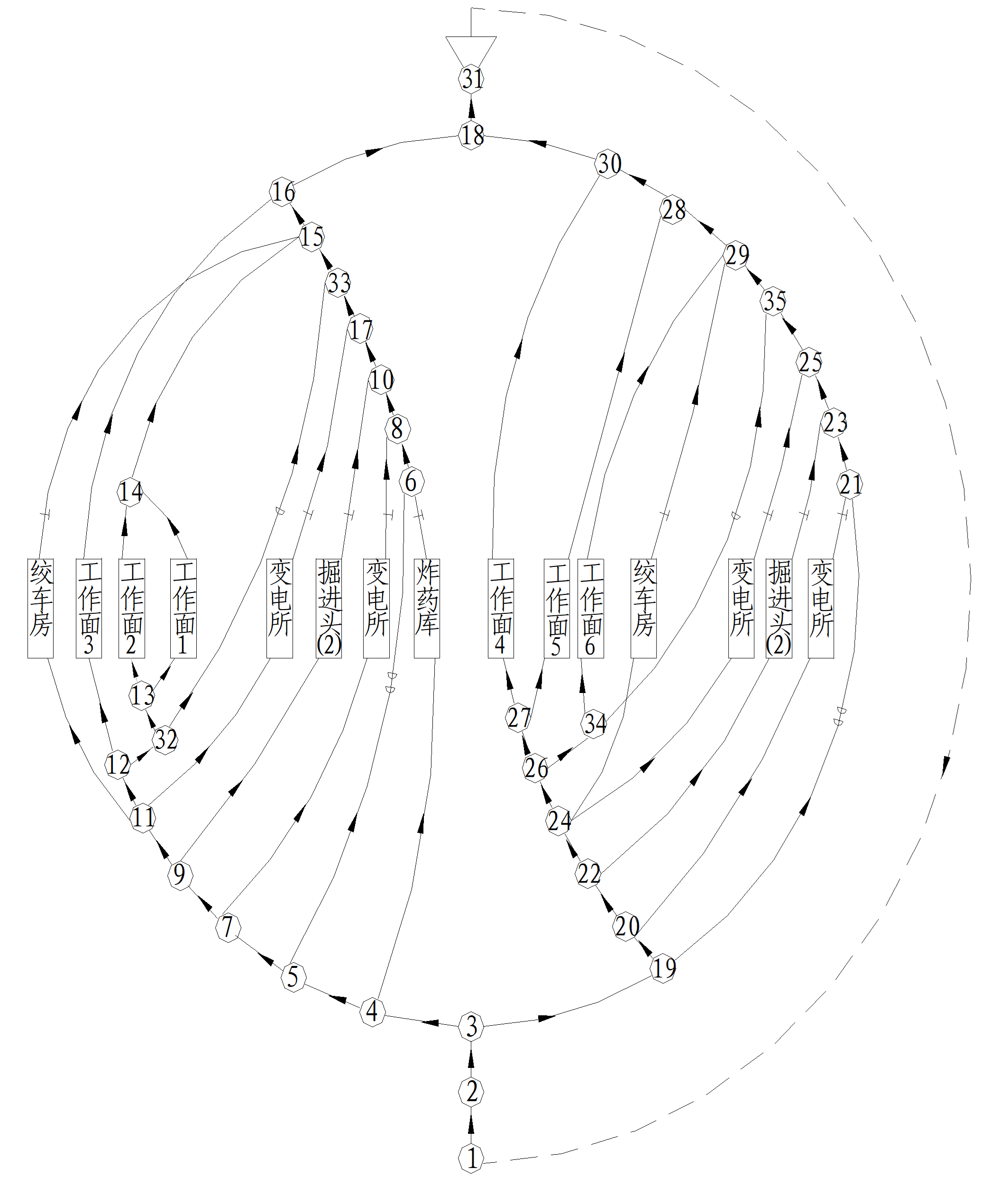
在矿井《矿井通风》课程中，我们已经学习到煤矿井下的巷道相互连接呈网络结构，而风流在巷道中流动，通过通风机提供动力，当自然分风无法满足风量分配要求时，进一步通过各种通风设施进行风量调节。一般将矿井通风系统抽象为单连通的有向图（Directed Graph），即通风网络图，如图1所示。

矿井通风网络图示例
图1 矿井通风网络图示例

图（Graph）是图论（一个数学分支）的主要研究对象，它是由若干给定的节点（也称顶点）及连接两节点的分支（也称边）所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系。通风网络图中不存在环（两端点相同的分支），但可能存在平行分支（有公共起点并有公共终点的两条分支）。图论已经系统地给出了图的数学表示和相关计算，因此可以据此构建通风网络图的数学模型。假设通风网络图中有 m 个节点，n 条分支，以列向量分别表示图的节点和分支所构成的集合：

$$ \boldsymbol{V}=\left[ v_i \right] =\left[ \begin{matrix} v_1& v_2& \cdots& v_m\\ \end{matrix} \right] ^{\mathrm{T}} $$

$$ \boldsymbol{E}=\left[ e_j \right] =\left[ \begin{matrix} e_1& e_2& \cdots& e_n\\ \end{matrix} \right] ^{\mathrm{T}} $$

其中 vi 表示编号为 i 的节点，ej 表示编号为 j 的分支。为了表述方便，也常用两个下标表示分支，如 eij 表示从节点 vi 到节点 vj 的分支。这里 V 和 E 以加粗、斜体的形式表示，表明他们不是单值标量，而是包含多个分量的向量或矩阵，下面的符号表示同样采用此法，将不再解释。

图中节点和分支的关系可用关联矩阵（Incidence matrix）表示：

$$ \boldsymbol{M}=\left[ b_{ij} \right] =\left[ \begin{matrix} b_{11}& b_{12}& \cdots& b_{1n}\\ b_{21}& b_{21}& \cdots& b_{2n}\\ \vdots& \vdots& \ddots& \vdots\\ b_{m1}& b_{m2}& \cdots& b_{mn}\\ \end{matrix} \right] $$

对于有向图，上式中 bij 的取值为：

$$ b_{ij}=\left\{ \begin{matrix} 1,& \text{当}e_j\text{以}v_i\text{为起点};\\ -1,& \text{当}e_j\text{以}v_i\text{为终点};\\ 0,& \text{其他}.\\ \end{matrix} \right. $$

如图2中左侧为一个有向图，右侧为其关联矩阵。可以看出，该矩阵每列的代数和均为 0。

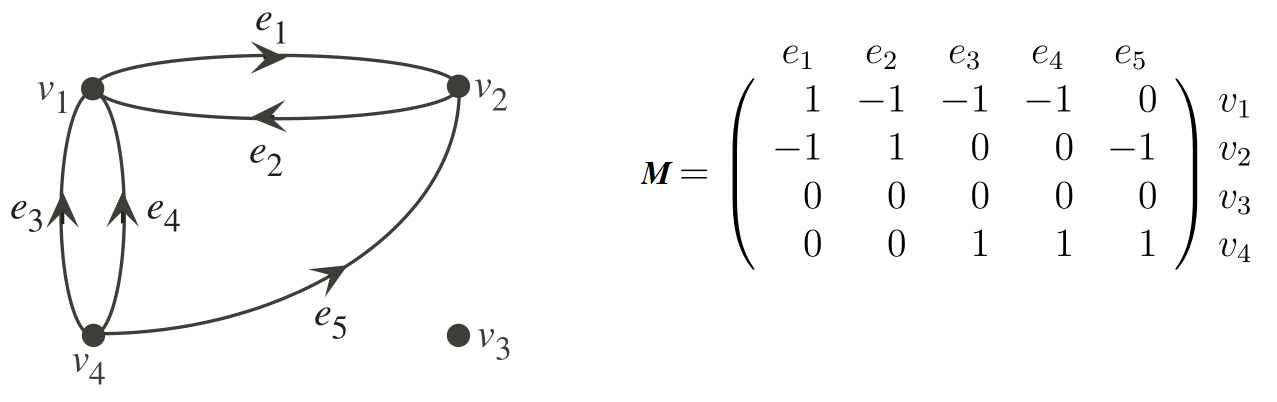
有向图的关联矩阵
图2 有向图的关联矩阵

根据图论知识，连通图的关联矩阵的秩 rank(M) = m – 1 ，即关联矩阵 M 的各行是线性相关的。从关联矩阵 M 中去掉任意一行，得到各行线性无关的矩阵，称为基本关联矩阵，记作 B。

将各种通风参数看作是与通风网络图的分支 E 或节点 V 关联的数据，以列向量表示这些参数。定义在分支上的参数有风阻 R(e)、风量 Q(e)、通风阻力 hR(e)、风机风压 hf(e)、自然风压 HN(e) 等，定义在节点上的参数有节点绝对全压 Pt(v)、相对全压 ht(v)、重力位能 EP(v) 等。这些参数的带圆括号的上标 (e) 和 (v) 仅起指示作用，并无任何计算意义。其中上标 (e) 表示该参数是定义在分支上的向量，其元素个数为 n；上标 (v) 表示该参数是定义在节点上的向量，其元素个数为 m。这些向量的分量的下标标注方法与节点、分支的下标标注方法相同，如 Pt i 表示第 i 个节点的全压，Qi 表示第 i 个分支的风量，而 Qij 表示从节点 vi 到节点 vj 的分支的风量。分支中风量 Q(e)、风机风压 hf(e) 和自然风压 HN(e) 具有方向性，在建模时假定他们的方向都与分支方向相同，当他们实际的方向与分支方向相反时，这些参数将取负值。

3.2 构建通风系统方程组

矿井通风系统中空气流动遵循风量守恒定律和能量守恒定律，通风网络建模的主要任务就是用方程以解析的形式描述这些定律。井巷内空气的流动是一个非常复杂的力学过程，为了便于建模和求解，必须对该过程做大幅度的简化，这些包括：将井巷内空气视作不可压缩的牛顿流体，将其流动视作一维定常流，空气的流态为紊流。

3.2.1 风量守恒定律

风量守恒定律可分别针对节点或割集用不同的方法进行表述，这里针对节点进行表述：单位时间内流入与流出某节点的各分支的空气质量的代数和等于零。

由于已将空气看作是不可压缩的，这里直接用体积流量代替质量流量，得如下方程：

$$\Sigma q_{ij}-\Sigma q_{jk}=0$$ (1)

式中， qij 和 qjk分别为与节点 vj 关联的分支 eij 和 ejk 的风量，m3/s。

上式可表示为矩阵形式：

$$\boldsymbol{MQ}^{\left( \mathrm{e} \right)}=\mathbf{0}^{\left( \mathrm{v} \right)}$$ (2)

式中，0(v) 是元素个数等于图节点个数 m 的零向量。

3.2.2 能量守恒定律

能量守恒定律可分别针对分支或回路用不同的方法进行表述，这里针对分支进行表述：通风网络中任一分支的通风阻力，等于该分支两端点间全压差、分支自然风压及分支中通风机风压的代数和。

该定律可表示为：

$$h_{Rij}-(p_i-p_j)-h_{Nij}-h_{fij}=0$$ (3)

式中：

根据通风阻力定律，当井巷内风流状态为紊流时，式(3)中的通风阻力项 hRij 为：

$$h_{Rij}=r_{ij}q_{ij}\left| q_{ij} \right|$$ (4)

式中：

式(3)中的通风机风压项 hf ij 是由通风机的个体特性曲线决定的，流过通风机不同的风量，将会有不同的通风机风压 hf ij。为了便于计算，一般事先经过回归分析，将 hf ij 表示为风量 qij 的高次多项式：

$$h_{f\mathrm{ }ij}=\mathrm{sign}\left( q_{ij} \right) \left( c_nq_{ij}^{n}+c_{n-1}q_{ij}^{n-1}+\cdots +c_1q_{ij}+c_0 \right)$$ (5)

式中：

由于式(5)的长度较大，在后续的公式推导中，并不使用其展开式的形式，而仍然使用 hf ij。

本次设计中忽略式(3)中的自然风压项 hNij。

将式(4)代入式(3)，可得：

$$r_{ij}q_{ij}\left| q_{ij} \right|-(p_i-p_j)-h_{Nij}-h_{fij}=0$$ (6)

上式也可以表示为矩阵形式：

$$ \mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) \boldsymbol{Q}^{\left( \mathrm{e} \right)}-\boldsymbol{M}^{\mathrm{T}}\boldsymbol{P}_{t}^{\left( \mathrm{v} \right)}-\boldsymbol{H}_{N}^{\left( \mathrm{e} \right)}-\boldsymbol{H}_{f}^{\left( \mathrm{e} \right)}=\mathbf{0}^{\left( \mathrm{e} \right)} $$ (7)

式中：

3.2.3 通风网络方程组

联立风量守恒方程式(2)和能量守恒方程式(7)，即得到描述通风网络的方程组为：

$$ \left\{ \begin{array}{c} \boldsymbol{MQ}^{\left( \mathrm{e} \right)}=\mathbf{0}^{\left( \mathrm{v} \right)}\\ \mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) \boldsymbol{Q}^{\left( \mathrm{e} \right)}-\boldsymbol{M}^{\mathrm{T}}\boldsymbol{P}_{t}^{\left( \mathrm{v} \right)}-\boldsymbol{H}_{N}^{\left( \mathrm{e} \right)}-\boldsymbol{H}_{f}^{\left( \mathrm{e} \right)}=\mathbf{0}^{\left( \mathrm{e} \right)}\\ \end{array} \right. $$ (8)

3.2.4 方程组的定解条件

实际的矿井通风网络解算多数是已知表征风网结构的关联矩阵 M、各个分支（巷道）的风阻 R(e)、自然风压 HN(e) 和通风机个体特性曲线 Hf(e)，求解各分支风量 Q(e) 和节点风压 Pt(v)（本设计仅对这种求解方式进行分析）。由于式(8)中 $\mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) \boldsymbol{Q}^{\left( \mathrm{e} \right)}$ 项和 Hf(e) 项都是分支风量 Q(e) 的非线性函数，因此整个方程组是一个非线性方程组，没法用线性代数中学到的线性方程组求解方法对此方程进行求解。

式(8)中的第 1、2 式分别包含 m、n 个方程。由于 rank(M) = m – 1，因此第 1 式中包含m - 1 个线性无关的方程。又由于 diag(M(e)) 这样的对角矩阵必然是满秩的，因此第 2 式包含 n 个线性无关的方程。这样线性无关的方程的总个数为 m + n – 1，而未知数包含 m 个节点全压和 n 个分支风量，共 m + n 个。未知数个数大于线性无关方程的个数，方程组是欠定的，将有无穷多个解。

为了使此方程组仅有有限个数的解，还需要再给定一个节点全压或分支风量值，通常是给定通风网络中大气节点的全压，即井口的大气压 P0。假设大气节点的编号为 r，则式(8)变为：

$$ \left\{ \begin{array}{c} \boldsymbol{MQ}^{\left( \mathrm{e} \right)}=\mathbf{0}^{\left( \mathrm{v} \right)}\\ \mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) \boldsymbol{Q}^{\left( \mathrm{e} \right)}-\boldsymbol{M}^{\mathrm{T}}\boldsymbol{P}_{t}^{\left( \mathrm{v} \right)}-\boldsymbol{H}_{N}^{\left( \mathrm{e} \right)}-\boldsymbol{H}_{f}^{\left( \mathrm{e} \right)}=\mathbf{0}^{\left( \mathrm{e} \right)}\\ P_{t\,\,r}=P_0\\ \end{array} \right. $$ (9)

式(9)中的最后一式相对于为式(8)添加了边界条件。在式(9)中，线性无关方程组个数和未知数个数都是 m + n，因此该方程组是良态的，其具有有限数量的解。注意，式(9)并非只有一个解，这和抛物线方程常常有两个解的情形类似。

接下来对于通风网络的解算问题，已经变为求解式(9)表示的非线性方程组问题了。

4 用牛顿法解算矿井通风网络方程组

式(9)这样的通风网络方程组的规模通常很大，因此一般只能进行数值解算。当方程组是零维时，一些通用的多变量非线性方程组的数值求解方法都同时适用于该方程的求解，最常用的是牛顿法以及各种拟牛顿法。相对于以往常用的通风网络求解的斯科特-恒斯雷法、京大二试法等，牛顿法具有数学逻辑较好、收敛速度快、对各种非线性方程（组）通用的优点。牛顿法的缺点是所得的解严重依赖所提供的初值，并且不能找出方程组所有的解。下面将推导用牛顿法求解式(9)的过程。

4.1 牛顿法介绍

牛顿法（Newton's method）又称为牛顿-拉弗森方法（Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数 f(x) 的泰勒级数的前面几项来寻找方程 f(x) = 0 的根。该方法同样可以用于方程组求解。

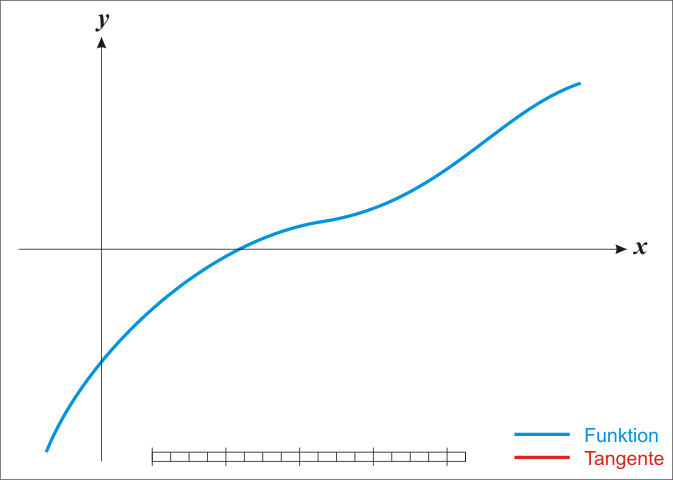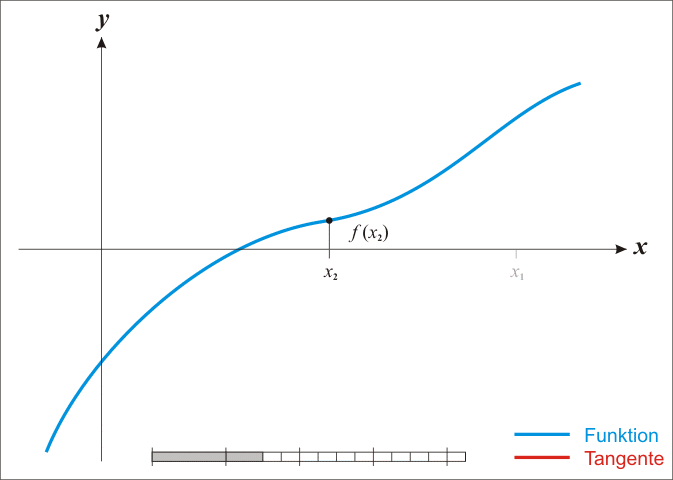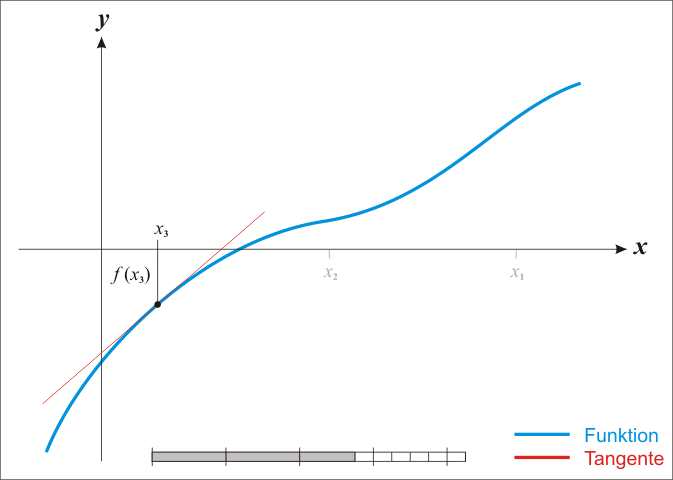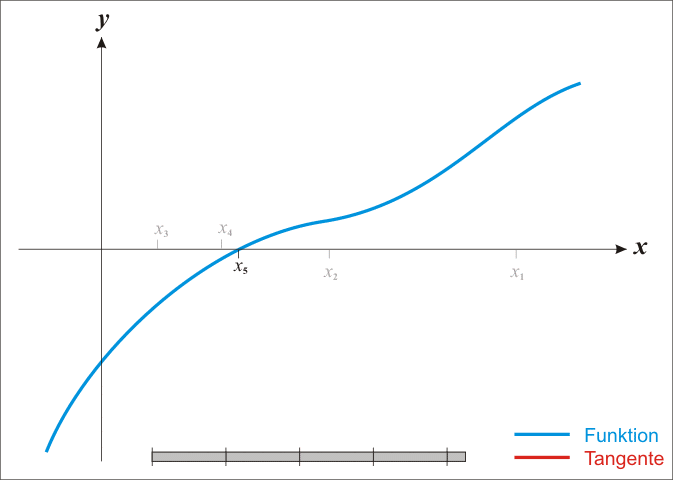
用牛顿法迭代求解方程的过程示意图
图3 用牛顿法迭代求解方程的过程示意图

对于如下具有 k 个变量和 l 个方程的连续可微方程组：

$$\boldsymbol{F}\left( \boldsymbol{x} \right) =\mathbf{0}$$

用牛顿法求解方程组的迭代步骤为：

$$ \left\{ \begin{array}{c} \boldsymbol{J}_F\left( \boldsymbol{x}_i \right) \boldsymbol{s}=-\boldsymbol{F}\left( \boldsymbol{x}_i \right)\\ \boldsymbol{x}_{i+1}=\boldsymbol{x}_i+\boldsymbol{s}\\ \end{array} \right. $$

式中：

$$ \boldsymbol{J}_F=\left[ \begin{matrix} \frac{\partial \boldsymbol{F}}{\partial x_1}& \frac{\partial \boldsymbol{F}}{\partial x_2}& \cdots& \frac{\partial \boldsymbol{F}}{\partial x_k}\\ \end{matrix} \right] =\left[ \begin{matrix} \frac{\partial F_1}{\partial x_1}& \frac{\partial F_1}{\partial x_2}& \cdots& \frac{\partial F_1}{\partial x_k}\\ \frac{\partial F_2}{\partial x_1}& \frac{\partial F_2}{\partial x_2}& \cdots& \frac{\partial F_2}{\partial x_k}\\ \vdots& \vdots& \ddots& \vdots\\ \frac{\partial F_l}{\partial x_1}& \frac{\partial F_l}{\partial x_2}& \cdots& \frac{\partial F_l}{\partial x_k}\\ \end{matrix} \right] $$

由以上介绍可以看出，在用牛顿法求解方程组时，首先解得方程组对应向量值函数 F(x) 的雅可比矩阵 JF，然后给定未知数的初值 x0（将其代入 xi），每次迭代时通过式 $\boldsymbol{J}_F\left( \boldsymbol{x}_i \right) \boldsymbol{s}=-\boldsymbol{F}\left( \boldsymbol{x}_i \right)$ 解得 s，进一步再通过式 $\boldsymbol{x}_{i+1}=\boldsymbol{x}_i+\boldsymbol{s}$ 求得下一个迭代值 xi + 1，如此反复迭代直到误差足够小。除了求解雅克比矩阵 JF，其他步骤均可以数值计算软件代为完成。

4.2 通风网络方程组对应的雅可比矩阵

对于式(9)，其分支风量 Q(e) 和节点风压 P(v) 按如下方式组成为未知数向量：

$$ \boldsymbol{x}=\left[ \begin{array}{c} \boldsymbol{Q}^{\left( \mathrm{e} \right)}\\ \boldsymbol{P}_{t}^{\left( \mathrm{v} \right)}\\ \end{array} \right] $$

为了推导得出式(9)对应的雅克比矩阵，将该式中第 1 式左侧函数记为 S，将第 2 式左侧函数记为 E。即有：

$$ \left\{ \begin{array}{c} \boldsymbol{S}=\boldsymbol{MQ}^{\left( \mathrm{e} \right)}\\ \boldsymbol{E}=\mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) \boldsymbol{Q}^{\left( \mathrm{e} \right)}-\boldsymbol{M}^{\mathrm{T}}\boldsymbol{P}_{t}^{\left( \mathrm{v} \right)}-\boldsymbol{H}_{N}^{\left( \mathrm{e} \right)}-\boldsymbol{H}_{f}^{\left( \mathrm{e} \right)}\\ \end{array} \right. $$

S 的第 i 行所对应的雅可比矩阵行向量为：

$$ \boldsymbol{J}_{S_i}=\left[ \begin{matrix} \frac{\partial s_i}{\partial q_1}& \frac{\partial s_i}{\partial q_2}& \cdots& \frac{\partial s_i}{\partial q_j}\cdots& \frac{\partial s_i}{\partial q_n}& 0_1& 0_2\cdots& 0_m\\ \end{matrix} \right] $$

式中：

由于 $\frac{\partial s_i}{\partial q_j}=m_{ij}$，S 对应的雅克比矩阵为：

$$ \boldsymbol{J}_S=\left[ \begin{matrix} \boldsymbol{M}& \mathbf{0}_{m\times m}\\ \end{matrix} \right] $$

E 的第 i 行所对应的雅可比矩阵行向量为：

$$ \boldsymbol{J}_{E_i}=\left[ \begin{matrix} \frac{\partial E_i}{\partial Q_1}& \frac{\partial E_i}{\partial Q_2}& \cdots& \frac{\partial E_i}{\partial Q_j}\cdots& \frac{\partial E_i}{\partial Q_n}& \frac{\partial E_i}{\partial P_{t1}}& \frac{\partial E_i}{\partial P_{t2}}& \cdots& \frac{\partial E_i}{\partial P_{tk}}\cdots& \frac{\partial E_i}{\partial P_{tm}}\\ \end{matrix} \right] $$

式中：

E 中各项对 Q(e) 的偏导数具有如下规律：

  1. E 中 diag(R(e))diag(|Q(e)|)Q(e) 项只是分支风量的函数，故该项中第 i 个元素对 Qj 的偏导数可分为两种情况：当 i ≠ j 时，其偏导数为 0；当 i = j 时，偏导数为 2Rj|Qj|。
  2. E 中 HN(e) 项基本不受风量和全压的影响，故其偏导数总为 0。
  3. E 中 Hf(e) 项中第 i 个元素对 Qj 的偏导数可分为两种情况：当 i ≠ j 时，其偏导数为 0；当 i = j 时，其偏导数为 $\frac{\partial H_{fi}}{\partial Q_i}$（具体形式根据风机个体特性曲线回归方程的形式求导确定）。

因此，E 中各行对 Q(e) 的偏导数为：

$$ \frac{\partial E_i}{\partial Q_j}=\left( 2\mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) -\mathrm{diag}\left( \boldsymbol{H}_{f,Q}^{\left( \mathrm{e} \right)} \right) \right) _{ij} $$

E 中仅有 MTPt(v) 项对 Pt(v) 的偏导数不为零，从而 E 中各行对 Pt(v) 的偏导数为：

$$ \frac{\partial E_i}{\partial P_{tk}}=-\left( \boldsymbol{M}^{\mathrm{T}} \right) _{ik} $$

E 对应的雅克比矩阵为：

$$ \boldsymbol{J}_E=\left[ \begin{matrix} 2\mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) -\mathrm{diag}\left( \boldsymbol{H}_{f,Q}^{\left( \mathrm{e} \right)} \right)& -\boldsymbol{M}^{\mathrm{T}}\\ \end{matrix} \right] $$

注意，上式的矩阵由两项构成（不要将其看作是一项），其中 MT 是末项，它和前面一项没有减法关系。

拼接 JS 和 JE，得到式(9)左侧的向量值函数对应的雅可比矩阵为：

$$ \boldsymbol{J}_F=\left[ \begin{matrix} \boldsymbol{M}& \mathbf{0}_{m\times m}\\ 2\mathrm{diag}\left( \boldsymbol{R}^{\left( \mathrm{e} \right)} \right) \mathrm{diag}\left( \left| \boldsymbol{Q}^{\left( \mathrm{e} \right)} \right| \right) -\mathrm{diag}\left( \boldsymbol{H}_{f,Q}^{\left( \mathrm{e} \right)} \right)& -\boldsymbol{M}^{\mathrm{T}}\\ \end{matrix} \right] $$ (10)

5 矿井通风网络的计算机建模和解算

以上所给出的通风网络方程组及其牛顿法求解过程涉及大量的矩阵运算，尤其是大规模的线性代数运算。这些运算如果只用编程语言的基础功能（如用 Python 的列表表示矩阵）来建模和求解，是极其困难的，而需要借助某些科学计算软件包（如 Python + NumPy + SciPy 或 MATLAB）。以下文档叙述基于 Python 的 NumPy 和 SciPy 包进行矿井通风网络的计算机建模与解算。

5.1 配置开发环境

NumPy 是使用 Python 进行科学计算的基础包。它为 Python 提供了一个强大多维数组对象，各种派生对象（如掩码数组和矩阵），以及一系列对数组进行快速操作的例程，包括数学、逻辑、形状操作、排序、选择、I/O、离散傅立叶变换、基本线性代数、基本统计操作、随机模拟，等等。当将 Python 用于科学和工程领域时，几乎都要用到此包。

SciPy 是构建在 NumPy 之上的数学算法和常用函数的集合。其不同的子包对应不同的应用，如插值、积分、优化、图像处理、统计、特殊函数等。这里我们主要使用 SciPy 中最优化子包 optimize 中用于非线性方程组求解的 fsolve 函数。

像 NumPy 和 SciPy 这类科学计算软件包一般包含 FORTRAN、C、C++ 等语言编写的二进制编译文件依赖，因此直接用 Python 自带的包安装器 pip 安装并不容易。NumPy 的官网提供了该包的多种安装方法，对于 Windows 操作系统，其中最简单的方法就是直接安装 Anaconda 科学计算平台，这是一个包管理器、一个环境管理器、一个 Python 数据科学发行版以及众多开源包的集合，其中当然也包含 NumPy 和 SciPy。本次课程设计将使用这个开发平台，请从官网下载其安装包（比较大，大约 800MB，而 Python 安装包才 25MB 左右）并按照提示安装。在安装完成后，Windows 操作系统的开采菜单将会出现“Anaconda3 (64-bit)”组，其他包含多个启动项，我们这里只需要选择“Anaconda Prompt”或“Anaconda Powershell Prompt”启动项，就可以像正常安装 Python 那样通过命令行使用 Python 解释器。另外，还需要设置 VS Code 或 PyCharm 开发环境，使其使用的 Python 解释器正好就是刚刚安装 Anaconda 的位置（例如：anaconda3\python.exe）。

5.2 相关技术介绍

前面已经说过，在通风网络方程组（式(9)）和其相应的雅克比矩阵（式(10)）中，存在大量的向量和矩阵。这些向量和矩阵并不是用 Python 基础的一维列表、二维列表来表示，而是用 NumPy 中定义的一维数组、二维数组（矩阵）来表示。NumPy 还提供了操作这些数组的基础函数，详情请见 NumPy 的文档。

在求解非线性方程组时，则需要使用 scipy.optimize.fsolve 函数，该函数实际上是对著名 MINPACK 库的 hybrd 和 hybrj 算法的封装。该函数返回一个由 func(x) = 0 定义的（非线性）方程组在一个初始估计值 x0 附近的根。封装后 fsolve 函数的签名如下：

scipy.optimize.fsolve(func, x0, args=(), fprime=None, full_output=0, col_deriv=0, xtol=1.49012e-08, maxfev=0, band=None, epsfcn=None, factor=100, diag=None)

可以看出，fsolve 的签名非常复杂。鉴于该函数的重要性，现将其英文文档翻译为中文：

参数：

返回值：

5.3 核心代码分析

为了降低编程的难度，这里给出了程序的核心代码，并对代码给出了大量的注释，请从此链接下载，并进行解压（如果解压到 D 盘根目录，则不用对代码进行任何修改）。本小节进一步对源代码进行解释。

首先，mine_vertilation_network.py 代码文件的开头是如下 3 行：

import os
import numpy as np
from scipy.optimize import fsolve

导入 os 模块是为了使用 os.chdir 函数；接下来一行不仅导入了 numpy 包，并将其重命名为 np；scipy 包的内容很多，我们只需要使用其中的 optimize 子包的 fsolve 函数。

os.chdir('D:/mine_vertilation_network')
incidence_matrix_path = 'incidence_matrix.csv'  # 关联矩阵 M
edge_resistances_path = 'edge_resistances.csv'  # 分支风阻 R
incidence_matrix = np.loadtxt(incidence_matrix_path, dtype=np.int64, delimiter=',')
edge_resistances = np.loadtxt(edge_resistances_path, dtype=np.float64, delimiter=',')

我们并不想把建模数据写死在源代码中，而是把重要的建模数据，如关联矩阵、分支风阻分别放到 incidence_matrix.csv 和 edge_resistances.csv 文件中，这使我们可以使用 Excel 或 VS Code 编辑其中的数据。然后在代码中使用 np.loadtxt 分别将这两个文件中的数据载入到 incidence_matrix 和 edge_resistances 变量中，这两个变量分别是矩阵和向量。

(node_num, edge_num) = incidence_matrix.shape
x_num = node_num + edge_num

这两行分别计算了节点数 node_num（关联矩阵的行数，前面的 m 值）和分支数 edge_num（关联矩阵的列数，前面的 n 值），这时通过调用 incidence_matrix 的 shape 属性得到的，该属性返回一个整型元组，其各个元素分别为多维数组各个维度的元素个数。node_num 和 edge_num 之和正好就是方程未知数的个数 x_num（m + n）。我们提前把这些数值算出来，以方便后续调用。

surface_pressure = 0.0
ref_node_index = 0

在前面得出的数学模型中，我们假定第 r 个节点的风压 Pt r 为参考节点的风压，并一般以矿井地表空气对应的节点作为 r 节点。在实际建模中，一般习惯将大气节点作为第一个节点，其索引 ref_node_index 为 0，其对应的全压 surface_pressure 为 0.0Pa。当然，这两个值都是可以改变的，只是我们还没有来得及不将他们编死在代码中。

fans = [{'ni': 3, 'a': 0.0, 'b': 0.0327, 'c': -18.464, 'd': 1146.3},
{'ni': 4, 'a': 0.0, 'b': -0.1971, 'c': 18.75, 'd': -18.322}]

这两行关于通风机的参数也是暂时编死在代码中的。一般可使用一元二次、一元三次方程组描述通风机个体特性曲线，形如：

$$ h_f=aq^3+bq^2+cq+d $$

矿井中只有少数巷道存在通风机，因此描述通风机时，只需要给出其对应的节点索引 ni，以及各个通风机个体特性曲线的参数 a、b、c 和 d 即可。本模型中有两个通风机，其所在分支的索引分别为 3 和 4。这两个通风机的三次项参数 a 都为 0.0，说明实际上用一元二次方程组就可以描述他们的个体特性曲线。

flowrates_init = 30.0 * np.ones(edge_num, dtype=np.float64)  # 风量初值
pressures_init = -50.0 * np.ones(node_num, dtype=np.float64)  # 全压初值
pressures_init[ref_node_index] = surface_pressure  # 设置地面节点的全压
x0 = np.concatenate((flowrates_init, pressures_init))

这 4 行设置了未知数的初始估计值。这种批量设置初值的方法极为粗糙，实际设置初值时有更多复杂的技巧，不过暂时能用就行。在实际计算中，我们设置的初值可能并不能得出满意的计算结果，如对于抽出式通风，计算所得的节点相对全压存在大量大于 0 的值显然是不合理的，这里只能手工尝试设置不同的初值，直到满意为止。风量初值和风压初值都属于未知数 x0 的初值，我们通过 np.concatenate 将他们拼接在一起。

def mvn_func(x):
    """该函数根据迭代过程中临时得出的 x 向量自动计算通风网络方程中的向量函数值 F(x)，该方程用于 fslove() 函数中的 func 参数"""

    # 未知数 x 的前 edge_num 项为分支风量 flowrates，后面各项为节点全压 pressures。
    # pressures 中第 ref_node_index 项为地面节点的全压，该项风压总是不变的，因此需要在每个循环中重新设定
    flowrates = x[:edge_num]  # 分支风量
    pressures = x[edge_num:]  # 节点全压
    pressures[ref_node_index] = surface_pressure  # 地面节点全压

    # 计算 M×Q
    f_nodes = incidence_matrix @ flowrates
    # 计算 diag(R)×diag(|Q|)×Q - M'×P
    f_edges = (np.diag(edge_resistances) @ np.diag(np.abs(flowrates)) @ flowrates) - (incidence_matrix.T @ pressures)
    # 计算通风机风压，并附加的特定节点的 f_edges 上
    for fan in fans:
        ni = fan.get('ni')
        ri = abs(flowrates[ni])
        f_edges[ni] -= fan.get('a') * pow(ri, 3) + fan.get('b') * pow(ri, 2) + fan.get('c') * ri + fan.get('d')

    # 拼接通风网络方程组中左侧函数值的两项，得到函数值向量
    f = np.concatenate((f_nodes, f_edges))
    return f

mvn_func(x) 函数与式(9)所示的通风网络方程组左侧向量函数相对应。该函数的参数 x 即为待求解的变量，它由 fsolve 在迭代过程中自动求得，我们需要根据 x 计算式(9)左侧部分的值。由于该式分为多个部分，为了计算方便，我们也把 x 切分为风量向量 flowrates 和风压向量 pressures，分别计算各个节点对应的风量守恒方程左侧向量 f_nodes，以及各个分支对应的能量守恒方程左侧向量 f_edges。后者的计算要更复杂一点，因为我们要对通风机 fans 进行变量，将其产生的风压附加的分支上。最后，将这两个向量的值拼接在一起并返回。

np.diag() 函数的作用是将一个向量转换为对角矩阵，np.abs() 函数的作用则是计算数组中各个元素的绝对值，并重新构造一个数组。尤其需要注意的是，在 NumPy 中，a * b 并不是执行矩阵乘法，而是将两个等尺寸的矩阵的对应元素相乘，或者将一个矩阵的每个元素乘以一个标量（即所谓的广播），a @ b 执行的才是矩阵乘法。

def mvn_jac_func(x):
    """该函数根据迭代过程中临时得出的 x 向量自动计算通风网络方程中的向量函数值 F(x) 的雅克比矩阵，该方程用于 fslove() 函数中的 fprime 参数"""

    flowrates = x[:edge_num]
    # 拼接 M 和 0 (m×m），得到雅克比矩阵的第一行，axis=1 参数表示对列进行拼接
    f_jac_nodes = np.concatenate((incidence_matrix, np.zeros((node_num, node_num))), axis=1)

    # 计算 2×diag(R)×diag(|Q|) 项
    f_jac_edges = 2.0 * (np.diag(edge_resistances) @ np.diag(np.abs(flowrates)))
    # 计算 diag(Hf) 项
    for fan in fans:
        ni = fan.get('ni')
        ri = abs(flowrates[ni])
        f_jac_edges[ni] -= 3 * fan.get('a') * pow(ri, 2) + 2 * fan.get('b') * ri + fan.get('c')
    # 将雅克比矩阵中第二行的两项进行拼接，得到雅克比矩阵的第二行，axis=1 参数表示对列进行拼接
    f_jac_edges = np.concatenate((f_jac_edges, -1.0*incidence_matrix.T), axis=1)

    # 拼接雅克比矩阵中的两行，得到整个雅克比矩阵
    f_jac = np.concatenate((f_jac_nodes, f_jac_edges))
    return f_jac

mvn_jac_func(x) 函数与式(10)所示的雅克比矩阵相对应。该函数的实现方式和前面的 mvn_func(x) 整体类似。

(root, infodict, ier, mesg) = fsolve(mvn_func, x0, fprime=mvn_jac_func, full_output=True)
# (root, infodict, ier, mesg) = fsolve(mvn_func, x0, full_output=True)

前面已经铺垫好了，在此处进行方程组的求解。这两行值需要使用其中一个就行。前者显式给出了雅克比矩阵，后者由系统自动估算雅克比矩阵值。由于前者能精确计算雅克比矩阵，因此其速度要更快一点。如果使用后者，则完全不必定义前面的 mvn_jac_func(x) 函数。通过为 fsolve() 函数提供 full_output=True，使返回值变为 4 个（否则只有一个 root），这样可以基于这些返回值作出更多的判断。

if ier:
    print('求解成功！\n各分支风量：')
    for i in range(edge_num):
        print(f'{i}:\t{root[i]:.3f}')

    print('各节点风压：')
    for i in range(node_num):
        print(f'{i}:\t{root[edge_num + i]:.3f}')
else:
    print('求解失败！\n错误信息为：\n', mesg)

最后，当我们判断 fsolve 执行成功时（ier 的值为 1），打印求解结果，否则打印错误信息。

6 解算示例

为了验证所编写程序的正确性，同时练习如何进行通风网络解算，这里给出一个相对较复杂的解算示例。图4为该示例对应的肥城查庄煤矿1985年通风网络图，这个示例同时被文献 [1] 和 [2] 先后用于验通风网络解算算法的正确性。 。

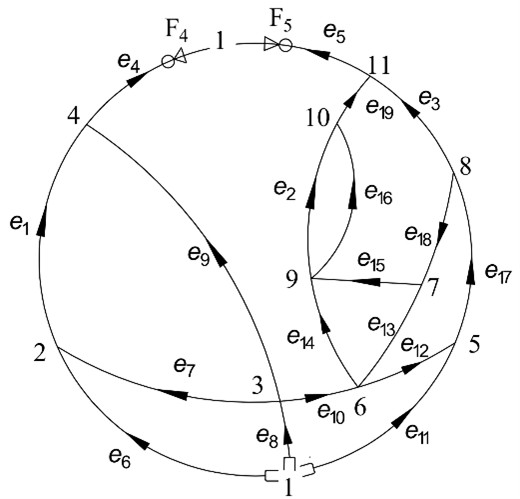
肥城查庄煤矿1985年通风网络图
图4 肥城查庄煤矿1985年通风网络图

在图4中，共有11个节点（m = 11），19个分支（n = 19）。注意图中的分支、节点的编号从 1 开始起算，而前面程序中分支、节点的索引从 0 开始起算。该图对应的关联矩阵为：

incidence_matrix = [
        [0, 0, 0, -1, -1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
        [1, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 1, -1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [-1, 0, 0, 1, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 1, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 1, 1, 1, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 1, 0, 0, -1, 0],
        [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 1, 0],
        [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, -1, 1, 0, 0, 0],
        [0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 1],
        [0, 0, -1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1]
    ]

该矩阵可通过 mine_vertilation_network/edge_resistances.csv 文件输入。

图中各分支的风阻为：

edge_resistances = [0.168012409, 0.287305363, 0.355303599, 0.00825, 0.0058, 0.0232, 0.0528, 0.00338, 0.2588, 0.00589, 0.0502, 0.0103, 0.0108, 0.1716, 0.0526, 0.0388, 0.0081, 0.025, 0.0395]

该向量可通过 mine_vertilation_network/edge_resistances.csv 文件输入。

图中的分支 4、分支 5（实际分别对应索引为 3 和 4 的分支）各有一个通风机。风机特性描述如下：

根据以上数据，对风机风量和风压数据进行多项式回归，得 F4 和 F5 风机的特性方程（风量—风压关系曲线）分别为：

$$h_{f4} = 0.0327q^2 - 18.464q + 1146.3\\ h_{f5} = -0.1971q^2 + 18.75q - 18.322$$

这两个风机的个体特性曲线参数已经在前面的代码中输入了。

根据这些已知条件，编制如前述的解算程序，最终解算结果为：

求解成功！
各分支风量：
0:      31.202
1:      13.601
2:      24.201
3:      56.359
4:      74.813
5:      29.189
6:      2.014
7:      76.057
8:      25.157
9:      48.886
10:     25.927
11:     3.351
12:     26.707
13:     18.829
14:     31.783
15:     37.011
16:     29.278
17:     5.076
18:     50.612
各节点风压：
0:      0.000
1:      -19.766
2:      -19.552
3:      -183.341
4:      -33.744
5:      -33.628
6:      -41.331
7:      -40.687
8:      -94.465
9:      -147.613
2:      -19.552
3:      -183.341
4:      -33.744
5:      -33.628
6:      -41.331
7:      -40.687
8:      -94.465
9:      -147.613
10:     -248.793

该结果与两个文献中的解算结果基本一样，说明该程序是正确的。

7 参考文献

  1. 辽宁省煤炭研究所. 解算矿井通风网路的DJS—6机ALGOL—60语言程序[J]. 煤矿安全, 1978(1): 23–35.
  2. 李恕和, 王义章. 矿井通风网络计算的牛顿法[J]. 煤炭学报, 1982(4): 52–62.