1. 体积力和体积力强度

作用于单位体积微团上的体积力称为体积力强度，其数学表达式为

地球引力的体积力强度为 $\rho \boldsymbol{g}$。体积力的合力为

体积力的合力矩为

2. 表面力和应力

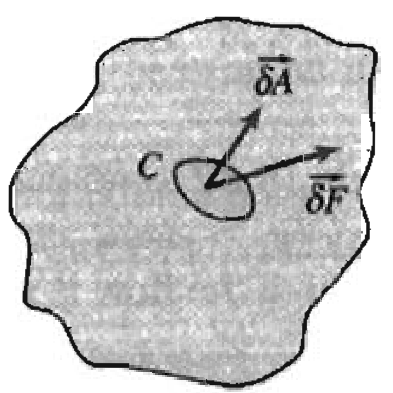
表面力不同于体积力，它分布于流体微团的表面，是一种接触力。

微元面积 $\delta A$ 上单位面积的表面力称为表面力的局部强度，又称为应力，定义如下

$$\boldsymbol{\sigma }^{\left( \boldsymbol{n} \right)}=\underset{\delta A\rightarrow 0}{\lim}\frac{\delta \boldsymbol{F}}{\delta A}$$

式中，$\delta \boldsymbol{F}$ 是面积 $\delta A$ 上的作用力，$\boldsymbol{\sigma }^{\left( \boldsymbol{n} \right)}$ 表示应力向量，上标 $\boldsymbol{n}$ 表示面力作用面 $\delta A$ 的方向。

2. 表面力和应力

经过空间中一点有无限多个面，每个面上通常都对应不同的应力向量 $\boldsymbol{\sigma }^{\left( \boldsymbol{n} \right)}$。这些应力向量是各个面的单位法向量 $\boldsymbol{n}$ 的线性函数，即

$$\boldsymbol{T}^{\left( \boldsymbol{n} \right)}=\boldsymbol{n}\cdot \boldsymbol{\sigma }$$

式中，$\boldsymbol{\sigma }$ 称为柯西应力张量或真实应力张量，是连续介质力学里用现时构形描述的二阶应力张量。该应力张量是一个方阵：

$$ \boldsymbol{\sigma }=\left[ \begin{matrix} \sigma _{11}& \sigma _{12}& \sigma _{13}\\ \sigma _{21}& \sigma _{22}& \sigma _{23}\\ \sigma _{31}& \sigma _{32}& \sigma _{33}\\ \end{matrix} \right] \equiv \left[ \begin{matrix} \sigma _{xx}& \sigma _{xy}& \sigma _{xz}\\ \sigma _{yx}& \sigma _{yy}& \sigma _{yz}\\ \sigma _{zx}& \sigma _{zy}& \sigma _{zz}\\ \end{matrix} \right] \equiv \left[ \begin{matrix} \sigma _x& \tau _{xy}& \tau _{xz}\\ \tau _{yx}& \sigma _y& \tau _{yz}\\ \tau _{zx}& \tau _{zy}& \sigma _z\\ \end{matrix} \right] $$

2. 表面力和应力

一点的应力张量是一个实对称二阶张量。根据剪应力互等定理，总有

$$ \tau _{xy}=\tau _{yx} \\ \tau _{xz}=\tau _{zx} \\ \tau _{yz}=\tau _{zy} $$

因此，一点的应力张量有 9 个分量，但只有 6 个独立分量。

对于无粘性的理想流体，所有剪应力为零，从而可得出其在任何方向的正应力都相等，应力张量退化为一个标量，即流体的压强。

1. 流体的易流性

将上页公式改写为

$$\tau _{xy}=\mu \frac{\delta u}{\delta y}$$

式中，$\mu$ 称作动力粘度系数，其单位是泊，且有

1 泊 = 1 kg‧m^-1‧s^-1 = Pa‧s

有时还用动力粘性系数除以密度，得运动粘性系数

$$\nu =\frac{\mu}{\rho}$$

$\nu$ 的单位是 m²‧s^-1。

1. 流体的易流性

右面的物质具有比左面的物质较高的黏度。

2. 流体的压缩性

由于压强变化而引起流体密度的变化成为压缩性。气体和液体的压缩性具有明显的区别：气体具有明显的可压缩性；液体的可压缩性非常小，经常被认为是不可压缩的。

对于常见的气体，其不同状态下的宏观物理行为可大致用理想气体的状态方程描述：

$$p=\rho \frac{R}{M}T$$

式中，$p$ 为气体的压强，$\rho$ 为密度，$R$ 为理想气体常数，$M$ 为气体的莫尔质量，$T$ 为气体的绝度温度。该方程和实际的气体状态常有偏差，可以使用范德华方程得出对实际气体状态更准确的描述。

2. 流体的压缩性

流体的压缩性也可用体积模量 $K$ 来表示，该量又称不可压缩量。它是产生单位相对体积收缩所需的压强，即

$$K=-V\frac{\text{d}p}{\text{d}V}=\rho \frac{\text{d}p}{\text{d}\rho}$$

体积模量的单位是 Pa。例如，水的体积模量为 2.2×10⁹Pa；空气的绝热体积模量为 1.42×10⁵Pa，等温体积模量为 1.01×10⁵Pa。