硕士研究生课程
高等流体力学
金洪伟 & 徐刚
西安科技大学安全科学与工程学院
如何浏览?
- 从浏览器地址栏打开 https://zimo.net/lt/;
- 点击章节列表中的任一链接,打开相应的演示文稿;
- 点击链接打开演示文稿,使用空格键或方向键导航;
- 按f键进入全屏播放,再按Esc键退出全屏;
- 按Alt键同时点击鼠标左键进行局部缩放;
- 按Esc或o键进入幻灯片浏览视图。
请使用最新版本浏览器访问此演示文稿以获得更好体验。
第2章 流体运动学
目 录
- 流体运动学
- (不考虑受力)运用分析和几何描述方法来研究流体一般运动的性质。
第1节 描述流体运动的两种方法
- 欧拉描述法
- 在任意指定的时间逐点描述当地的运动特征量(如速度、加速度)及其他物理量(如压力、密度等)分布。
在选定的时空坐标系 $\left( \boldsymbol{x},t \right)$ 考察流动过程中力学和其他物理参量的分布。时空坐标 $\left( \boldsymbol{x},t \right)$ 是自变量,称作欧拉变量。各个物理参量是欧拉变量的函数,即
$$\boldsymbol{U}=\boldsymbol{U}\left( \boldsymbol{x},t \right) ,\quad T=T\left( \boldsymbol{x},t \right) ,\quad p=p\left( \boldsymbol{x},t \right)$$
欧拉法属于场描述法,上式中描述的这些参量就是不同时刻的速度场、温度场和压强场。
示例:在 t 时刻,A 点处流体质点的速度为……
第1节 描述流体运动的两种方法
- 拉格朗日描述法
- 从某个时刻开始跟踪每一个质点,记录这些质点的位置、速度、加速度和物理参数的变化。
通常用每个质点在初始时刻的坐标作为他们的“标记”,然后跟踪每个质点,在他们的运动轨迹上考察他们的物理状态。质点的初始时刻坐标 $\boldsymbol{A}$ 和时间变量 t 是自变量,称为拉格朗日变量。各个物理参量是拉格朗日变量的函数,即
$$\boldsymbol{x}=\boldsymbol{x}\left( \boldsymbol{A},t \right) ,\quad T=T\left( \boldsymbol{A},t \right) ,\quad p=p\left( \boldsymbol{A},t \right)$$
拉格朗日法属于跟踪质点的描述法。
示例:在 t 时刻,质点 A 的速度为……
第1节 描述流体运动的两种方法
拉格朗日描述法中的位移函数 $\boldsymbol{x}=\boldsymbol{x}\left( \boldsymbol{A},t \right)$ 就是质点的轨迹,它有以下两个基本性质:
在初始时刻
$$\boldsymbol{x}\left( \boldsymbol{A},0 \right) =\boldsymbol{A}$$
在任何时刻,质点位置变量 $\boldsymbol{x}$ 与该质点初始时刻的位置变量 $\boldsymbol{A}$ 是一一对应的连续函数。即存在 $\boldsymbol{x}=\boldsymbol{x}\left( \boldsymbol{A},t \right)$ 的反演
$$\boldsymbol{A}=\boldsymbol{A}\left( \boldsymbol{x},t \right)$$
通过上式可追踪 t 时刻任何位置 $\boldsymbol{x}$ 质点的初始位置 $\boldsymbol{A}$,从而实现欧拉变量 $\left( \boldsymbol{x},t \right)$ 和拉格朗日变量 $\left( \boldsymbol{A},t \right)$ 的转换。
第2节 流场的几何描述
流线和椭圆表示漩涡,蓝色和红色椭圆
分别表示顺时针和逆时针旋转的旋涡
用几何方法描述流场可以使我们直观和形象地了解流动状态。
第2节 流场的几何描述
1. 流线、流面和流管
- 流线(Streamline)
- 速度场的向量线。它是某一固定时刻的空间曲线,该曲线上任意一点的切向量与当地的速度向量重合。
根据定义,流线场在给定时间考察流动在空间的图像,它是一种欧拉速度场的描述方法。
给定某时刻的速度场,针对任意初始点对速度场进行积分,即可得到通过该初始点的流线。
1. 流线、流面和流管
假设流线的参数方程为
$$\boldsymbol{x}=\boldsymbol{r}\left( s \right)$$
则流线上任意点的切向量为 $\mathrm{d}\boldsymbol{r}$,同时流场当地速度为 $\boldsymbol{U}\left( \boldsymbol{x}, t_0 \right)$(欧拉表达式),根据流线的定义,两个向量是平行的,因此有流线方程
$$\mathrm{d}\boldsymbol{r}\times \boldsymbol{U}=\mathbf{0}$$
其展开形式为
$$\frac{\mathrm{d}x_1}{U_1\left( x_1, x_2, x_3, t_0 \right)}=\frac{\mathrm{d}x_2}{U_2\left( x_1, x_2, x_3, t_0 \right)}=\frac{\mathrm{d}x_3}{U_3\left( x_1, x_2, x_3, t_0 \right)}$$
1. 流线、流面和流管
- 流面
- 某一时刻通过给定曲线(该曲线不是流线)上每一点做流线所构成的曲面。
- 流管
- 某一时刻通过给定封闭曲线(该曲线不是流线)上每一点做流线所构成的流面。
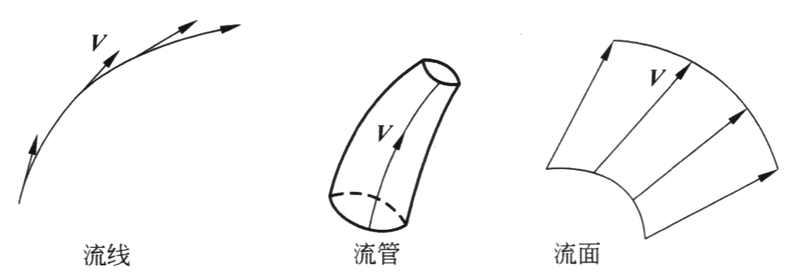
流面是由流线组成的空间曲面,流管是管状的流面。
2. 迹线
- 迹线(Pathline)
- 流体质点运动的轨迹,是质点在各个时刻所处位置连起来形成的曲线。
迹线的定义是建立在拉格朗日法基础上的,是追踪一个流体质点得到的。
流线是同一时刻,不同质点连接起来的速度场向量线。
迹线是同一质点在不同时刻的位移曲线。
3. 定常流和非定常流
与时间无关的欧拉速度场称为定常流,反之称为非定常流。
定常速度场的表达式中不含欧拉变量 $t$,只有位置变量 $\boldsymbol{x}$,即
$$\boldsymbol{U}=\boldsymbol{U}\left( \boldsymbol{x} \right)$$
定常流场的流线和迹线有以下性质:
- 在定常流场中过同一点的流线不随时间变化;
- 任意时刻通过同一点的迹线和流线重合。
第3节 质点的加速度公式和质点导数
1. 质点的加速度公式
质点的加速度是质点速度向量随时间的变化率。
在拉格朗日描述式中,位移函数 $\boldsymbol{x}\left( \boldsymbol{A},t \right)$,位移函数对时间 $t$ 求二次偏导数,就得到质点 $\boldsymbol{A}$ 的加速度
$$\boldsymbol{a}=\left( \frac{\partial ^2\boldsymbol{x}}{\partial t^2} \right)$$
1. 质点的加速度公式
欧拉描述法给出速度场 $\boldsymbol{U}\left( \boldsymbol{x},t \right)$,而不追踪质点,要由速度场计算 $\left( \boldsymbol{x},t \right)$ 处的质点加速度时必须求出该质点在 $\delta t$ 时间内的速度增量,然后求极值,即
$$\boldsymbol{a}=\underset{\delta \boldsymbol{x}\rightarrow 0,\delta t\rightarrow 0}{\lim}\left[ \frac{\boldsymbol{U}\left( \boldsymbol{x}+\delta \boldsymbol{x},t+\delta t \right) -\boldsymbol{U}\left( \boldsymbol{x},t \right)}{\delta t} \right]$$
将上式的分子作泰勒展开
$$\boldsymbol{U}\left( \boldsymbol{x}+\delta \boldsymbol{x},t+\delta t \right) -\boldsymbol{U}\left( \boldsymbol{x},t \right) = \\ \left( \frac{\partial \boldsymbol{U}}{\partial t} \right) _x\delta t+\left( \frac{\partial \boldsymbol{U}}{\partial x_1} \right) _t\delta x_1+\left( \frac{\partial \boldsymbol{U}}{\partial x_2} \right) _t\delta x_2+\left( \frac{\partial \boldsymbol{U}}{\partial x_3} \right) _t\delta x_3+\boldsymbol{O}\left( \delta t^2,\left| \delta \boldsymbol{x} \right|^2,\delta t\left| \delta \boldsymbol{x} \right| \right)$$
1. 质点的加速度公式
将上式代入加速度公式,并略去高阶小量,得
$$\boldsymbol{a}=\frac{\partial \boldsymbol{U}}{\partial t}+\frac{\partial \boldsymbol{U}}{\partial x_1}\frac{\partial x_1}{\partial t}+\frac{\partial \boldsymbol{U}}{\partial x_2}\frac{\partial x_2}{\partial t}+\frac{\partial \boldsymbol{U}}{\partial x_3}\frac{\partial x_3}{\partial t}=\frac{\partial \boldsymbol{U}}{\partial t}+U_1\frac{\partial \boldsymbol{U}}{\partial x_1}+U_2\frac{\partial \boldsymbol{U}}{\partial x_2}+U_3\frac{\partial \boldsymbol{U}}{\partial x_3}$$
上式还可写作
$$\boldsymbol{a}=\frac{\partial \boldsymbol{U}}{\partial t}+\left( \boldsymbol{U}\cdot \nabla \right) \boldsymbol{U}$$
$\frac{\partial \boldsymbol{U}}{\partial t}$ 是空间中一个固定点的速度变化率,而 $\boldsymbol{a}$ 是一个特定质点的速度变化率。即使 $\frac{\partial \boldsymbol{U}}{\partial t} = 0$,以致在给定点的速度不再变化,但仍可能有加速度。如以恒定速率沿一圆周流动的水正在作加速运动(具有向心加速度),尽管在一给定点的速度并不随时间发生变化,但其加速度仍可能不为零。
用欧拉法给出的速度场求加速度时
质点加速度 = 速度的局部导数 + 速度的迁移导数
上式中的加速度分为两部分:
- 局部导数 $\frac{\partial \boldsymbol{U}}{\partial t}$
- 给定空间点上的速度随时间的变化率。这一部分是因为流场的非定常性产生的。
- 对流导数或迁移导数 $\left( \boldsymbol{U}\cdot \nabla \right) \boldsymbol{U}$
- 因为 $\boldsymbol{U}\cdot \nabla =U_s\frac{\partial}{\partial s}$($s$ 是速度方向),它是沿速度方向的导数,或给定瞬时的速度场线方向的导数,这一部分是因为速度场不均匀性产生的。
第3节 质点的加速度公式和质点导数
2. 质点导数
将推导加速度公式的方法推广到质点上任意物理量增长率的计算,就有质点导数的概念。
- 质点导数
- 质点携带的物理量随时间的变化率。用 $\frac{\mathrm{D}}{\mathrm{D}t}$ 表示。
在欧拉描述法中任意物理量 $Q$ 的质点导数等于
$$\frac{\mathrm{D}Q}{\mathrm{D}t}=\frac{\partial Q}{\partial t}+\left( \boldsymbol{U}\cdot \nabla \right) Q$$
其中 $Q$ 可能是标量、向量或张量。
2. 质点导数
质点导数的运算也可用以下运算符表示
$$\frac{\mathrm{D}}{\mathrm{D}t}=\frac{\partial}{\partial t}+\boldsymbol{U}\cdot \nabla =\frac{\partial}{\partial t}+U_1\frac{\partial}{\partial x_1}+U_2\frac{\partial}{\partial x_2}+U_3\frac{\partial}{\partial x_3}$$
物理量的质点导数 =
物理量的局部导数 + 物理量的对流导数
局部导数 $\frac{\partial}{\partial t}$ 是物理量在欧拉变量 $\boldsymbol{x}=\left( x_1, x_2, x_3 \right)$ 不变的条件下的时间增长率;质点导数 $\frac{\mathrm{D}}{\mathrm{D}t}$ 是物理量在质点运动轨迹上的时间增长率。
定常流中,物理量的局部导数等于零,这时质点导数等于对流导数。
第4节 流体微团运动分析

连续介质受力后要发生变形,由于流体的易流性,流体运动过程中,流场各个微团除了移动和转动外,将发生持续的变形,而流体微团的变形状态和它的应力状态密切联系,为此我们需要对流体微团变形过程做仔细的研究。
第4节 流体微团运动分析
1. 柯西—亥姆霍兹流体微团速度分解定理
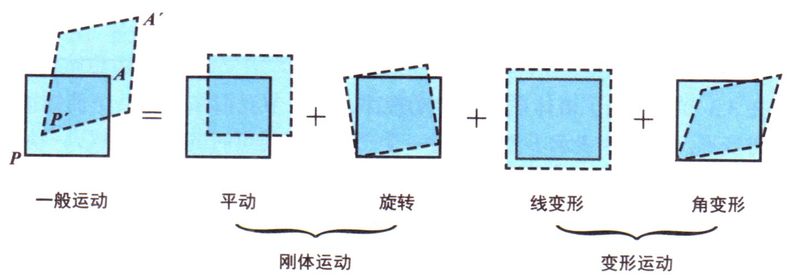
定理:流场 $\boldsymbol{U}\left( \boldsymbol{x},t \right)$ 中微团上任意一点的运动可以分解为平动、转动和变形三部分之和。
证明:设在流场 $\boldsymbol{U}\left( \boldsymbol{x},t \right)$ 中,在时刻 $t$ 任取一微团,微团上参考点 $\boldsymbol{x}_0$ 处的速度为 $\boldsymbol{U}_0=\boldsymbol{U}\left( \boldsymbol{x}_0,t \right)$,我们来考察微团上同一时刻任意一点 $\boldsymbol{x}=\boldsymbol{x}_0+\delta \boldsymbol{x}$ 的速度 $\boldsymbol{U}\left( \boldsymbol{x}_0+\delta \boldsymbol{x},t \right)$。
1. 柯西—亥姆霍兹流体微团速度分解定理
利用泰勒展开,有
$$\boldsymbol{U}\left( \boldsymbol{x}_0+\delta \boldsymbol{x},t \right) =\boldsymbol{U}\left( \boldsymbol{x}_0,t \right) +\frac{\partial \boldsymbol{U}}{\partial x_1}\delta x_1+\frac{\partial \boldsymbol{U}}{\partial x_2}\delta x_2+\frac{\partial \boldsymbol{U}}{\partial x_3}\delta x_3+O\left( \left| \delta \boldsymbol{x} \right|^2 \right)$$
忽略高阶小量后,微团上任意点的速度为
$$\boldsymbol{U}\left( \boldsymbol{x},t \right) =\boldsymbol{U}_0+\left( \frac{\partial \boldsymbol{U}}{\partial x_j} \right) \delta x_j$$
将上式进一步写成速度分量的形式
$$U_i\left( \boldsymbol{x},t \right) =U_{i0}+\left( \frac{\partial U_i}{\partial x_j} \right) _0\delta x_j$$
1. 柯西—亥姆霍兹流体微团速度分解定理
上式中 $\frac{\partial U_i}{\partial x_j}$ 代表一个二阶张量,它可以进一步分解为一个对称张量和一个反对称张量之和
$$\frac{\partial U_i}{\partial x_j}=\frac{1}{2}\left( \frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i} \right) +\frac{1}{2}\left( \frac{\partial U_i}{\partial x_j}-\frac{\partial U_j}{\partial x_i} \right) =S_{ij}+\Omega _{ij}$$
对称张量 $S _{ij}$ 的 6 个分量分别是流体微团的线变形速率和角变形速率;反对称张量 $\Omega _{ij}$ 的 3 个分量是流体微团的准刚体转动角速度的 3 个分量。
因此,流体微团上任意一点的速度可表示为
$$U_i=U_{i0}+\left( S_{ij} \right) _0\delta x_j+\left( \Omega _{ij} \right) _0\delta x_j$$
1. 柯西—亥姆霍兹流体微团速度分解定理
在直角坐标系中,张量 $\frac{\partial U_i}{\partial x_j}$ 的分解
$$ \left[ \begin{matrix} \frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}& \frac{\partial u}{\partial z}\\ \frac{\partial v}{\partial x}& \frac{\partial v}{\partial y}& \frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x}& \frac{\partial w}{\partial y}& \frac{\partial w}{\partial z}\\ \end{matrix} \right] =\left[ \begin{matrix} \frac{\partial u}{\partial x}& 0& 0\\ 0& \frac{\partial v}{\partial y}& 0\\ 0& 0& \frac{\partial w}{\partial z}\\ \end{matrix} \right] +\left[ \begin{matrix} 0& \frac{1}{2}\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \right)& \frac{1}{2}\left( \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} \right)\\ \frac{1}{2}\left( \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y} \right)& 0& \frac{1}{2}\left( \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y} \right)\\ \frac{1}{2}\left( \frac{\partial w}{\partial x}+\frac{\partial u}{\partial z} \right)& \frac{1}{2}\left( \frac{\partial w}{\partial y}+\frac{\partial v}{\partial z} \right)& 0\\ \end{matrix} \right] \\ +\left[ \begin{matrix} 0& \frac{1}{2}\left( \frac{\partial u}{\partial y}-\frac{\partial v}{\partial x} \right)& \frac{1}{2}\left( \frac{\partial u}{\partial z}-\frac{\partial w}{\partial x} \right)\\ \frac{1}{2}\left( \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} \right)& 0& \frac{1}{2}\left( \frac{\partial v}{\partial z}-\frac{\partial w}{\partial y} \right)\\ \frac{1}{2}\left( \frac{\partial w}{\partial x}-\frac{\partial u}{\partial z} \right)& \frac{1}{2}\left( \frac{\partial w}{\partial y}-\frac{\partial v}{\partial z} \right)& 0\\ \end{matrix} \right] $$
上式中右侧三项分别为流体微团的线变形、角变形和旋转运动。(请见后面证明与分析)
第4节 流体微团运动分析
2. 流体微团的变形率张量
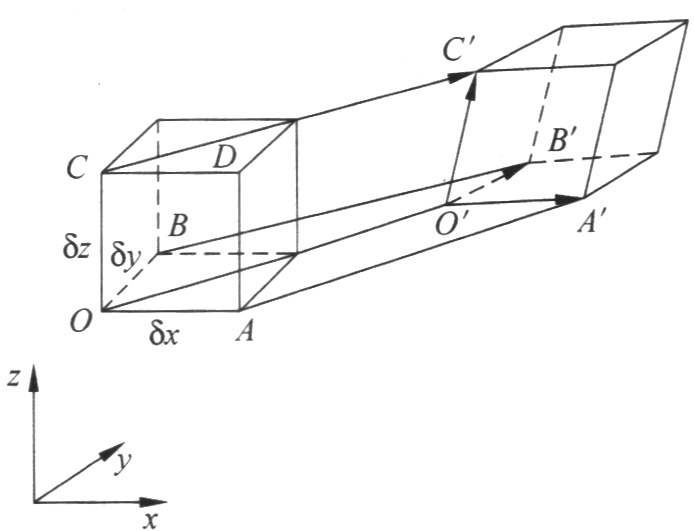
在时刻 $t$,取一长方体流体微团,长方体 $OABC$ 在 $\delta t$ 时刻后运动到 $O'A'B'C'$,它变形为近似平行六面体。微元体各边可能伸长或缩短,微元体的矩形表面可能因剪切而变为平行四边形。
可以通过向量运算计算出微元体上各顶点的位移 $\overrightarrow{OO'}$、$\overrightarrow{AA'}$、$\overrightarrow{BB'}$ 和 $\overrightarrow{CC'}$,以及各顶点相对 $O'$ 点的位置 $\overrightarrow{O'A'}$、$\overrightarrow{O'B'}$ 和 $\overrightarrow{O'C'}$。(过程略)
2. 流体微团的变形率张量
- 线变形率
- 单位时间内微元线段 $\delta x_i$ 的相对伸长。
$x$ 方向微元线段的伸长率为
$$\dot{\varepsilon} _x=\underset{\delta t\rightarrow 0}{\lim}\frac{\left| \overrightarrow{O'A'} \right|-\left| \overrightarrow{OA} \right|}{\left| \overrightarrow{OA} \right|\delta t}$$
对上式进行求解,可得
$$\dot{\varepsilon} _x=\frac{\partial u}{\partial x}$$
2. 流体微团的变形率张量
同理,可以证明
$$\dot{\varepsilon} _y=\frac{\partial v}{\partial y},\quad \dot{\varepsilon} _z=\frac{\partial w}{\partial z}$$
即直角坐标系中 $S_{ij}$ 张量的对角线分量分别表示所在方向的线变形率。
2. 流体微团的变形率张量
- 角变形率
- 微元平面上两垂直线段夹角在单位时间内减小量之半称为该面的角变形率。
$x-y$ 平面上的角变形率为
$$\dot{\gamma} _{xy}=\underset{\delta t\rightarrow 0}{\lim}\frac{\angle AOB-\angle A'O'B'}{2\delta t}$$
对上式进行求解,可得
$$\dot{\gamma} _{xy}=\frac{1}{2}\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \right)$$
2. 流体微团的变形率张量
同理,可以证明
$$\dot{\gamma} _{yz}=\frac{1}{2}\left( \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y} \right) ,\quad \dot{\gamma} _{zx}=\frac{1}{2}\left( \frac{\partial w}{\partial x}+\frac{\partial u}{\partial z} \right)$$
即直角坐标系中 $S_{ij}$ 张量的非对角线分量分别表示角变形率。
2. 流体微团的变形率张量
综上,对称张量 $S_{ij}$ 的 6 个分量是微团的线变形率和角变形率。即
$$ S_{ij}=\left[ \begin{matrix} \dot{\varepsilon} _1& \dot{\gamma} _{12}& \dot{\gamma} _{13}\\ \dot{\gamma} _{12}& \dot{\varepsilon} _2& \dot{\gamma} _{23}\\ \dot{\gamma} _{13}& \dot{\gamma} _{23}& \dot{\varepsilon} _3\\ \end{matrix} \right] ,\quad S_{ij}=\left[ \begin{matrix} \dot{\varepsilon} _x& \dot{\gamma} _{xy}& \dot{\gamma} _{xz}\\ \dot{\gamma} _{xy}& \dot{\varepsilon} _y& \dot{\gamma} _{yz}\\ \dot{\gamma} _{xz}& \dot{\gamma} _{yz}& \dot{\varepsilon} _z\\ \end{matrix} \right] $$
因此速度梯度张量的对称部分 $S_{ij}$ 又称变形率张量。
2. 流体微团的变形率张量
- 体积变化率
- 流体微团的体积变化率是单位时间内流体微团体积的相对增长率。
微团的体积变化率为
$$\dot{\varepsilon} =\underset{\delta t\rightarrow 0}{\lim}\frac{V\left( O'A'B'C' \right) -V\left( OABC \right)}{V\left( OABC \right) \delta t}$$
可以证明体积变化率为
$$\dot{\varepsilon} =\dot{\varepsilon} _x+\dot{\varepsilon} _y+\dot{\varepsilon} _z=S_{11}+S_{22}+S_{33}$$
或写成
$$\dot{\varepsilon} =S_{ii}$$
2. 流体微团的变形率张量
体积变化率实际上就是速度场的散度,即
$$\dot{\varepsilon} =\nabla \cdot \boldsymbol{U}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}$$
即微元体的体积变化率等于变形张量对角线上 3 项之和(又称张量的迹,也等于该点速度场散度,它是一个标量场。
当流体微团为不可压缩时,体积增长率等于零,也就是该点的速度场散度等于零。
2. 流体微团的变形率张量
从变形率张量中减去各向同性的体膨胀率称之为纯变形率张量:
$$S_{ij}^{'}=S_{ij}-\frac{1}{3}\dot{\varepsilon} \delta _{ij}$$
式中,$\delta _{ij}$ 是克罗内克函数
$$ \delta _{ij}=\left\{ \begin{matrix} 1& \left( i=j \right)\\ 0& \left( i\ne j \right)\\ \end{matrix} \right. $$
第4节 流体微团运动分析
3. 流体微团的准刚体转动角速度
通过几何分析,可得出流体微团绕 $x$、$y$ 和 $z$ 轴旋转的角速度分别为:
$$\Omega _x=\frac{1}{2}\left( \frac{\partial w}{\partial y}-\frac{\partial v}{\partial z} \right) ,\quad \Omega _y=\frac{1}{2}\left( \frac{\partial u}{\partial z}-\frac{\partial w}{\partial x} \right) ,\quad \Omega _z=\frac{1}{2}\left( \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} \right)$$
这 3 个角速度正好就是前面流体微团运动分解中反对称张量 $\Omega _{ij}$ 的 3 个独立分量。而同时这 3 个分量又是速度场旋度 $\nabla \times \boldsymbol{U}$ 的 3 个分量的一半。这说明反对称张量 $\Omega _{ij}$ 和速度场旋度之半是等价的,将 $\Omega _{ij}$ 称为准刚体角速度。
第4节 流体微团运动分析
综上,完成了柯西—亥姆霍兹流体微团速度分解定理,该定理可进一步表述为:
流体微团任意点的运动 = 参考点的移动(平动) + 体积膨胀运动(线变形) + 纯变形运动(角变形) + 准刚体转动(旋转)

第5节 流场的旋度
1. 涡量及其性质
- 涡量
- 速度场的旋度 $\nabla \times \boldsymbol{U}$ 又称涡量,用 $\boldsymbol{\omega }$ 表示。
由于旋度的散度 $\nabla \cdot \left( \nabla \times \boldsymbol{F} \right) =0$,因此:涡量场的散度等于零。即
$$\nabla \cdot \boldsymbol{\omega }=0$$
1. 涡量及其性质
- 涡线
- 涡量场的向量线称为涡线。涡线的切线和当地的涡量或准刚体角速度重合,所以涡线是流体微团准刚体转动方向的连线。形象地说,涡线像一根柔性轴把流体微团穿在一起。
- 涡面
- 给定瞬间,通过某一曲线(本身不是涡线)的所有涡线构成的曲面称为涡面。
- 涡管
- 管状涡面的内域称为涡管。
1. 涡量及其性质
- 涡通量
- 给定空间曲面,则下列面积分称为涡通量
- $$I=\iint_A{\boldsymbol{\omega }\cdot \boldsymbol{n}\mathrm{d}A}$$
- $\boldsymbol{n}$ 是曲面 $A$ 的外法线方向。$I > 0$,涡通量是正值;$I < 0 $,涡通量是负值。
- 涡管强度
- 涡管界面上涡通量的绝对值 $\left| I \right|$ 称为涡管强度。
1. 涡量及其性质
- 涡管强度守恒定理
- 给定瞬间涡管任意界面上的涡管强度相等。
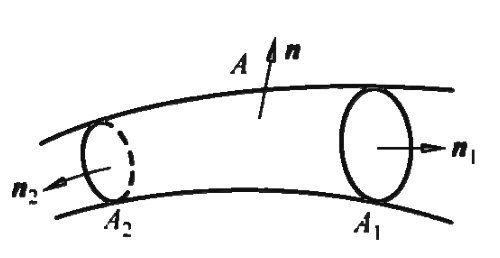
证明:略。
由涡管强度守恒定理可得出结论:在流场中涡管不能消失。流场中涡管只能有以下三种形式:
- 涡管两端延伸到无限远;
- 涡管形成封闭涡环;
- 涡管中止于物面或其他界面上。
2. 速度环量
- 速度环量
- 在速度场中沿封闭周线的线积分 $\oint_l{\boldsymbol{U}\cdot \mathrm{d}\boldsymbol{x}}$ 称作绕该周线的速度环量,记作 $\varGamma _l$。
定理:速度环量等于张在封闭周线 $l$ 上任意曲面的涡通量,其中曲面的法向量 $\boldsymbol{n}$ 由右手法则确定。
证明:根据斯托克斯公式,有
$$\oint_l{\boldsymbol{U}}\cdot \mathrm{d}\boldsymbol{x}=\iint_A{\left( \nabla \times \boldsymbol{U} \right) \cdot \boldsymbol{n}\mathrm{d}A}$$
$$\oint_l{\boldsymbol{U}}\cdot \mathrm{d}\boldsymbol{x}=\iint_A{\boldsymbol{\omega }\cdot \boldsymbol{n}\mathrm{d}A}$$
3. 无旋流动和速度势
- 无旋流场
- 速度旋度处处为零的流场。
$$\nabla \times \boldsymbol{U}=0$$
无旋流动的主要特性是速度场可以用一个标量函数的梯度表示,即无旋流动一定存在一势函数 $\varPhi \left( x, y, z \right)$,它的梯度等于流场速度:
$$\boldsymbol{U}=\nabla \varPhi$$
称 $\varPhi$ 为速度势。